题目内容
15.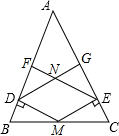 已知:如图,M是等腰三角形ABC的底边BC的中点,MD⊥AB,ME⊥AC,EF⊥AB,DG⊥AC,垂足分别为为D,E,F,G,DG与EF交于点N,求证:四边形DMEN是菱形.
已知:如图,M是等腰三角形ABC的底边BC的中点,MD⊥AB,ME⊥AC,EF⊥AB,DG⊥AC,垂足分别为为D,E,F,G,DG与EF交于点N,求证:四边形DMEN是菱形.
分析 先证明四边形DMEN是平行四边形,再证明MD=ME即可.
解答 证明:连接AM.
∵MD⊥AB,EF⊥AB,
∴EF∥MD,
∵ME⊥AC,DG⊥AC,
∴ME∥DG,
∴四边形DMEN是平行四边形,
∵AB=AC,BM=MC,
∴MA平分∠BAC,
∵MD⊥AB,ME⊥AC,
∴MD=ME,
∴四边形DMEN是菱形.
点评 本题考查菱形的判定和性质、角平分线的性质等知识,熟练掌握菱形的判定方法是解题的关键,记住①邻边相等的平行四边形是菱形②四边相等的四边形是菱形③对角线垂直的平行四边形是菱形,属于中考常考题型.

练习册系列答案
相关题目
5.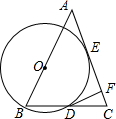 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
(1)求DC的长;(2)求AB的长.
 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.(1)求DC的长;(2)求AB的长.
6.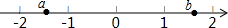 实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
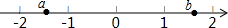 实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )| A. | -2$\sqrt{2}$ | B. | -2$\sqrt{3}$ | C. | 0 | D. | 2$\sqrt{3}$ |
20.a是$\sqrt{15}$-5的整数部分,则a为( )
| A. | -1 | B. | 1 | C. | 0 | D. | -2 |
4.下列式子不能因式分解的是( )
| A. | x2-4 | B. | 3x2+2x | C. | x2+25 | D. | x2-4x+4 |
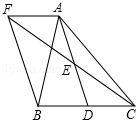 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.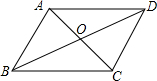 已知?ABCD,AC与BD相交于点O.
已知?ABCD,AC与BD相交于点O.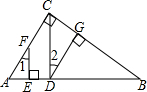 已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试判断CD与AB的位置关系,并说明理由.请完成下列解答:
已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试判断CD与AB的位置关系,并说明理由.请完成下列解答: