题目内容
14.已知O是?ABCD对角线的交点,△AOB的面积是2,则?ABCD的面积是8.分析 由平行四边形的对角线互相平分得出△BOC的面积=△COD的面积=△AOD的面积=△AOB的面积,即可求出?ABCD的面积.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴△BOC的面积=△COD的面积=△AOD的面积=△AOB的面积=2,
∴?ABCD的面积=4×2=8.
故答案是:8.
点评 本题考查了平行四边形的性质以及面积的计算方法;熟练掌握平行四边形的性质,得出△BOC的面积=△COD的面积=△AOD的面积=△AOB的面积是解决问题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
5.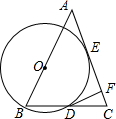 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
(1)求DC的长;(2)求AB的长.
 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.(1)求DC的长;(2)求AB的长.
9. 若实数a,b在数轴上的位置如图所示,则$\frac{b+1}{a+1}+\frac{b}{a}$的结果是( )
若实数a,b在数轴上的位置如图所示,则$\frac{b+1}{a+1}+\frac{b}{a}$的结果是( )
 若实数a,b在数轴上的位置如图所示,则$\frac{b+1}{a+1}+\frac{b}{a}$的结果是( )
若实数a,b在数轴上的位置如图所示,则$\frac{b+1}{a+1}+\frac{b}{a}$的结果是( )| A. | 正数 | B. | 零 | C. | 负数 | D. | 非正数 |
6.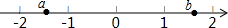 实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
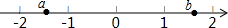 实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )| A. | -2$\sqrt{2}$ | B. | -2$\sqrt{3}$ | C. | 0 | D. | 2$\sqrt{3}$ |
4.下列式子不能因式分解的是( )
| A. | x2-4 | B. | 3x2+2x | C. | x2+25 | D. | x2-4x+4 |

 已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.
已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.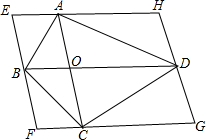 如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.
如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.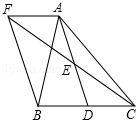 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.