题目内容
11.平行四边形ABCD中,AB=5,EF=2,∠A、∠D的平分线交BC于E、F,则BC=12或8.分析 根据平行四边形的性质结合角平分线的性质得出FC=DC,同理可得:AB=BE,进而画出符合题意的图形求出答案.
解答 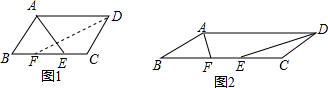 解:如图1所示:∵平行四边形ABCD中,∠A、∠D的平分线交BC于E、F,
解:如图1所示:∵平行四边形ABCD中,∠A、∠D的平分线交BC于E、F,
∴∠ADF=∠CDF,∠ADF=∠CFD,AB=DC=5,
∴∠CFD=∠CDF,
∴FC=DC,
同理可得:AB=BE=5,
∵EF=2,
∴BE+FC-EF=BC=10-2=8,
如图2,由(1)得:AB=BF,DC=EC,
则BE+EF+EC=BC=5+5+2=12.
故答案为:12或8.
点评 此题主要考查了平行四边形的性质以及角平分线的性质,正确得出AB=BE,DC=FC是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.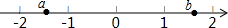 实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
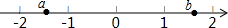 实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )| A. | -2$\sqrt{2}$ | B. | -2$\sqrt{3}$ | C. | 0 | D. | 2$\sqrt{3}$ |
20.a是$\sqrt{15}$-5的整数部分,则a为( )
| A. | -1 | B. | 1 | C. | 0 | D. | -2 |
 已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.
已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.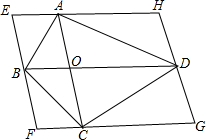 如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.
如图,在四边形ABCD中,对角线AC、BD交于点O.过它的四个顶点分别作两条对角线的平行线相交于点E、F、G、H.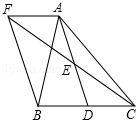 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.