题目内容
11.关于x的方程$\frac{1+x}{1-x}$=-$\frac{a}{b}$(a≠b)的解是x=$\frac{a+b}{a-b}$.分析 方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:去分母得:b(1+x)=-a(1-x),
去括号、移项合并得:(a-b)x=a+b,
∵a+b≠0,
解得:x=$\frac{a+b}{a-b}$,
经检验x=$\frac{a+b}{a-b}$是分式方程的解.
故答案为:x=$\frac{a+b}{a-b}$.
点评 此题考查了分式方程的解,以及解分式方程,需注意在任何时候都要考虑分母不为0.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
3.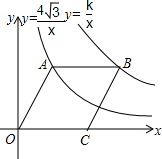 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )| A. | 6$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 9$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
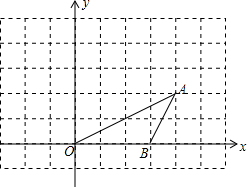 如图所示,在平面直角坐标系中,点A、B的坐标分别为(4,2)和(3,0),将△OAB绕原点O按逆时针方向旋转90°到△OA′B′.
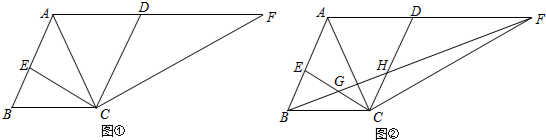
如图所示,在平面直角坐标系中,点A、B的坐标分别为(4,2)和(3,0),将△OAB绕原点O按逆时针方向旋转90°到△OA′B′. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2cm,试求出AE的长度.
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2cm,试求出AE的长度.