题目内容
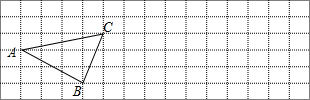
6．
如图，为了计算河的宽度，某学习小组在河对岸选定一个目标点A，再在河岸的这一边选取点B和点C，使AB⊥BC，然后再选取点E，使E C⊥BC，用视线确定BC和AE的交点D．此时如果测得BD=160 米，DC=80米，E C=49米，求A、B间的距离．
分析 根据题意得出△ABD∽△ECD，进而利用相似三角形的性质得出AB的长．
解答 解：由题意可得：∠ABD=∠ECD=90°，∠ADB=∠EDC，
则△ABD∽△ECD，
故$\frac{BD}{DC}$=$\frac{AB}{EC}$，
即$\frac{160}{80}$=$\frac{AB}{49}$，
解得：AB=98，
答：A、B间的距离为98m．
点评 此题主要考查了相似三角形的应用，根据题意得出相似三角形是解题关键．
练习册系列答案
相关题目
如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB，若BE=2cm，试求出AE的长度．
已知直线a∥b∥c，直线m，n与直线a，b，c分别交于点A，C，E，B，D，F，AC=4，CE=6，BD=3，则BF=7.5．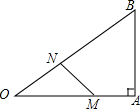
如图，在Rt△OAB中，∠A=90°，OA=4，AB=3，动点M从点A出发，动点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒$\frac{5}{4}$个单位长度的速度，沿OB向终点B移动．设运动时间为t秒．