题目内容
8．有三张牌的牌面数字是2，3，4现在把它们洗匀，数字朝下放在桌上，从中随机抽出一张记下牌面的数字放回，然后再从随机抽出一张记下牌面数字，则两次抽出牌的牌面数字的和不是2的倍数的概率为$\frac{4}{9}$．分析 画出树状图知：所有可能出现的结果共有9种，两次抽出牌的牌面数字的和不是2的倍数的结果有4个，即可得出结果．
解答 解：画树状图如下：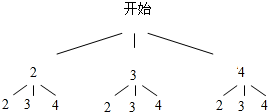
由树状图知：所有可能出现的结果共有9种，两次抽出牌的牌面数字的和不是2的倍数的结果有4个，
∴两次抽出牌的牌面数字的和不是2的倍数的概率为$\frac{4}{9}$；
故答案为：$\frac{4}{9}$．
点评 本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．
练习册系列答案
相关题目
3．
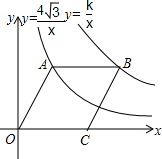如图，点A在双曲线y=$\frac{4\sqrt{3}}{x}$（x＞0）上，点B在双曲线y=$\frac{k}{x}$（x＞0）上（点B在点A的右侧），且AB∥x轴，若四边形OABC是菱形，且∠AOC=60°，则k等于（ ）
如图，点A在双曲线y=$\frac{4\sqrt{3}}{x}$（x＞0）上，点B在双曲线y=$\frac{k}{x}$（x＞0）上（点B在点A的右侧），且AB∥x轴，若四边形OABC是菱形，且∠AOC=60°，则k等于（ ）| A． | 6$\sqrt{3}$ | B． | 8$\sqrt{3}$ | C． | 9$\sqrt{3}$ | D． | 12$\sqrt{3}$ |
基础问题：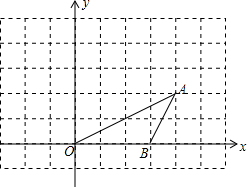
如图所示，在平面直角坐标系中，点A、B的坐标分别为（4，2）和（3，0），将△OAB绕原点O按逆时针方向旋转90°到△OA′B′．
已知直线a∥b∥c，直线m，n与直线a，b，c分别交于点A，C，E，B，D，F，AC=4，CE=6，BD=3，则BF=7.5．