题目内容
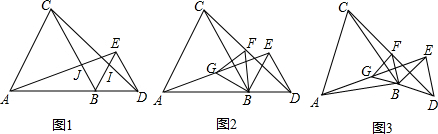
14.(1)如图1,线段AD上一点B,分别以AB,BD为边在线段AD的同侧作等边△ABC,等边△BDE,连接AE,CD,求证:BI=BJ.(2)如图2,将(1)中其他条件不变,若F,G分别是AE,CD的中点,连接GB,FB,求证:GF=GB.
(3)如图3,将(2)中其它条件不变,若A、B、D三点不在同一条直线时,第(2)中的结论成立吗?请先写出结论,然后证明.
分析 (1)利用SAS证明△CBD与△ABE全等,再证明△BDI与△BEJ全等即可;
(2)利用SAS证明△FCB与△GAB全等,再利用全等三角形的性质证明即可;
(3)利用SAS证明△ABE与△CBD全等,再利用SAS证明△GBE与△FBD全等,得出等边三角形GBF,即可得出.
解答 证明:(1)∵∠CBD=∠CBE+∠EBD=∠CBE+60°,∠ABE=∠CBE+∠ABC=∠CBE+60°,
∴∠CBD=∠ABE,
∵BD=BE,BC=AB,
在△CBD与△ABE中,
$\left\{\begin{array}{l}{BD=BE}\\{∠CBD=∠ABE}\\{BC=AB}\end{array}\right.$,
∴△CBD≌△ABE(SAS),
∴∠BDI=∠BEJ,
∵∠CBE=180°-∠CBA-∠DBE=180°-60°-60°=60°=∠EBD,
在△BDI与△BEJ中,
$\left\{\begin{array}{l}{∠BDI=∠BEJ}\\{∠CBE=∠EBD}\\{BD=BE}\end{array}\right.$,
∴△BDI≌△BEJ(AAS),
∴BI=BJ;
(2)在△FCB与△GAB中,
$\left\{\begin{array}{l}{CF=AG}\\{∠FCB=∠GAB}\\{BC=AB}\end{array}\right.$,
∴△FCB≌△GAB(SAS),
∴GB=FB;
(3)成立,理由如下:
∵∠ABC=∠EBD=60°,
∴∠ABC+∠CBE=∠EBD+∠CBE,
∴∠ABE=∠CBD,
在△ABE与△CBD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBD}\\{BC=BD}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴AE=CD,∠AEB=∠CDB;
∵G,F分别为AE,CD的中点,
∴GE=FD,
在△GBE与△FBD中,
$\left\{\begin{array}{l}{GE=FD}\\{∠AEB=∠CDB}\\{BE=BD}\end{array}\right.$,
∴△GBE≌△FBD(SAS),
∴GB=BF,∠GBE=∠FBD,
∠GBE-∠FBE=∠FBD-∠FBE,
∴∠GBF=∠EBD=60°,
∴△GBF是等边三角形,
∴GF=GB.
点评 此题考查全等三角形的判定和性质,关键是利用SAS证明三角形全等,利用全等三角形的性质进而证明.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | x≠-1 | B. | x≠0 | C. | x≠1 | D. | x>1 |
| A. | 2 | B. | ±2 | C. | -2 | D. | 不存在 |
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数分布直方图 |
 如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.
如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.