题目内容
2.“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.我市某运动商城的自行车销售量自2014年起逐月增加,据统计,该商城2月份销售自行车100辆,4月份销售了144辆.(1)若该商城自行车销量的平均月增长率相同,求平均月增长率:
(2)考虑到自行车需求不断增加,该商城准备投入4.2万元再购进一批两种规格的自行车,已知A型车的进价为600元/辆,售价为1000元/辆,B型车进价为1200元/辆,售价为1500元/辆.根据销售经验,A型车销量超过B型车的2倍,但不超过B型车的2.6倍.请你通过计算,为商城选择最佳进货方案.
分析 (1)设该商城2、3月份的月平均增长率为x.等量关系为:2月份的销售量×(1+增长率)2=4月份的销售量,把相关数值代入求解即可.
(2)设A型车x辆,根据“A型车不少于B型车的2倍,但不超过B型车的2.6倍”列出不等式组,求出x的取值范围;然后求出利润W的表达式,根据一次函数的性质求解即可.
解答 解:(1)设平均月增长率x,根据题意列方程:
100(1+x)2=144,
解得x1=-2.2=-220%(不合题意,舍去),x2=0.2=20%,
答:平均月增长率20%;
(2)设购进A型车x辆,则购进B型车$\frac{42000-600x}{1000}$辆,
根据题意得:2×$\frac{42000-600x}{1000}$≤x≤2.6×$\frac{42000-600x}{1000}$,
解得:38$\frac{2}{11}$≤x≤42$\frac{21}{32}$
利润W=(1000-600)x+$\frac{42000-600x}{1000}$(1500-1200)=1260+220x.
∵220>0,∴W随着x的增大而增大.
当x=42时,$\frac{42000-600x}{1000}$=28(辆).
答:为使利润最大,该商城应购进42辆A型车和28辆B型车.
点评 本题考查了一元二次方程、一元一次不等式组和一次函数的应用,解题关键是根据题意列出方程或不等式,这也是本题的难点.

练习册系列答案
相关题目
13.与$\sqrt{6}$最接近的整数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.用线段a,b,c作为三角形的三边,下列哪种情况不构成直角三角形( )
| A. | a=5,b=12,c=13 | B. | a:b:C=1:2:$\sqrt{3}$ | C. | a=8,b=9,c=10 | D. | a=b=3,c=3$\sqrt{2}$ |
17.抛物线y=-2(x+6)2+5的顶点坐标是( )
| A. | (6,5) | B. | (-6,5) | C. | (6,-5) | D. | (-2,5) |
11.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
则这50名学生这一周在校的平均体育锻炼时间是6.4小时.
| 时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 10 | 15 | 20 | 5 |
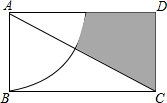 如图,矩形ABCD的长AD为2$\sqrt{3}$,宽AB为2,若以A点为圆心,AB为半径作出扇形,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(用含π的式子表示)
如图,矩形ABCD的长AD为2$\sqrt{3}$,宽AB为2,若以A点为圆心,AB为半径作出扇形,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(用含π的式子表示)