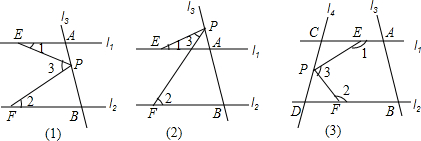题目内容
9. 如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.
如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.
分析 作FH∥CD,根据平行线的性质求出∠HFQ的度数,根据EF⊥AB,得到∠EGB=90°,根据平行线的性质求出∠EFH的度数即可.
解答  解:作FH∥CD,
解:作FH∥CD,
∴∠HFQ=∠1=30°,
又∵∠EGB=90°,
∴∠EFH=∠EGB=90°,
∴∠EFQ=∠EFH+∠HFQ=120°.
答:∠F的度数是120°.
点评 本题重点考查了平行线的性质,掌握两直线平行,同位角相等、内错角相等和同旁内角互补是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
17.抛物线y=-2(x+6)2+5的顶点坐标是( )
| A. | (6,5) | B. | (-6,5) | C. | (6,-5) | D. | (-2,5) |
18.已知点A(-2,y1)、B(1,y2)、C(4,y3)都在函数y=x2-4x-5的图象上,则比较y1、y2、y3的大小正确的是( )
| A. | y2<y3<y1 | B. | y3<y1<y2 | C. | y1<y3<y2 | D. | y2<y1<y3 |
19. 如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )
如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )
 如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )
如图,正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则EB比EA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |