题目内容
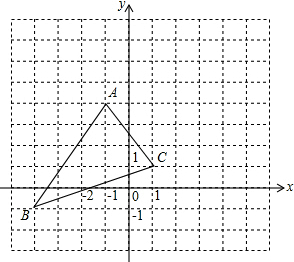
5.如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第5个图案需要的棋子数为( )
| A. | 61 | B. | 91 | C. | 152 | D. | 169 |
分析 依次求得n=1,2,3,…,图案需要的棋子枚数.再根据规律以此类推,可得出第n个图案需要的棋子枚数,进一步代入求得答案即可.
解答 解:∵n=1时,总数是6+1=7;
n=2时,总数为6×(1+2)+1=19;
n=3时,总数为6×(1+2+3)+1=37枚;
…;
∴n=n时,有6×(1+2+3+…n)+1=6×$\frac{n(n+1)}{2}$+1=3n2+3n+1枚.
∴n=5时,总数为6×(1+2+3…+5)+1=91枚.
故选:B.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.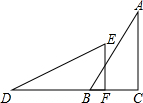 如图,△ABC≌△DEF,∠C=∠DFE=90°,A与D是 对应点,要使△DEF通过几何变换与△ABC重合,必须有的变换是( )
如图,△ABC≌△DEF,∠C=∠DFE=90°,A与D是 对应点,要使△DEF通过几何变换与△ABC重合,必须有的变换是( )
 如图,△ABC≌△DEF,∠C=∠DFE=90°,A与D是 对应点,要使△DEF通过几何变换与△ABC重合,必须有的变换是( )
如图,△ABC≌△DEF,∠C=∠DFE=90°,A与D是 对应点,要使△DEF通过几何变换与△ABC重合,必须有的变换是( )| A. | 轴对称 | B. | 平移 | C. | 旋转 | D. | 中心对称 |
15.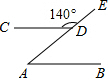 如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
 如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
如图,AB∥CD,∠CDE=140°,则∠A的度数为( )| A. | 70° | B. | 65° | C. | 50° | D. | 40° |
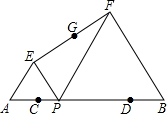 如图:已知AB=16,点C、D在线段AB上且AC=DB=3; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是( )
如图:已知AB=16,点C、D在线段AB上且AC=DB=3; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是( )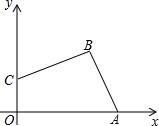 如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2)
如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2)