题目内容
13.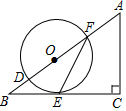 如图,在△ABC中,∠C=90°,D,F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,∠OFE=$\frac{1}{2}$∠A.
如图,在△ABC中,∠C=90°,D,F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,∠OFE=$\frac{1}{2}$∠A.(1)求证:BC是⊙O的切线;
(2)若sinB=$\frac{1}{2}$,求∠FEC.
分析 (1)首先连接OE,由在△ABC中,∠C=90°,FG⊥BC,可得FG∥AC,又由∠OFE=$\frac{1}{2}$∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;
(2)由sinB=$\frac{1}{2}$,得到∠B=30°,根据三角形的内角和得到∠BOE=60°,根据等腰三角形的性质得到∠OFE=∠OEF,根据三角形的外角的性质即可得到结论.
解答 (1)证明:连接OE,
∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,
∴FG∥AC,
∴∠OFG=∠A,
∴∠OFE=$\frac{1}{2}$∠OFG,
∴∠OFE=∠EFG,
∵OE=OF,
∴∠OFE=∠OEF,
∴∠OEF=∠EFG,
∴OE∥FG,
∴OE⊥BC,
∴BC是⊙O的切线;
(2)∵sinB=$\frac{1}{2}$,
∴∠B=30°,
∴∠BOE=60°,
∵OF=OE,
∴∠OFE=∠OEF,
∵∠BOE=∠OFE+∠OEF=60°,
∴∠OEF=30°,
∴∠FEC=60°.
点评 此题考查了切线的判定、等腰三角形的性质、三角函数等知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
3.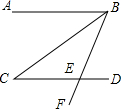 如图,已知AB∥CD,BC平分∠ABE,∠C=30°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=30°,则∠CEF的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=30°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=30°,则∠CEF的度数是( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
1.将直线y=$\frac{1}{2}$x+1向右平移4个单位后得到直线y=kx+b,则k+b的值为( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
8.下列图形中,不是中心对称图形的是( )
| A. | 平行四边形 | B. | 圆 | C. | 等边三角形 | D. | 正六边形 |
18.下列计算结果为a6的是( )
| A. | a•a5 | B. | a8-a2 | C. | (a3)3 | D. | 4a8÷3a2 |
2. 如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )
如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )
 如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )
如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )| A. | (-2m,-2n) | B. | (2m,2n) | C. | (-2n,-2m) | D. | (2n,2m) |
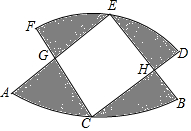 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是$\widehat{AB}$的中点,若扇形的半径为3,则图中阴影部分的面积等于$\frac{9π}{2}$-9.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是$\widehat{AB}$的中点,若扇形的半径为3,则图中阴影部分的面积等于$\frac{9π}{2}$-9.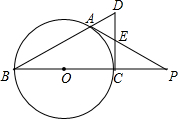 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD得中点E,AE的延长线与BC的延长线交于点P.
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD得中点E,AE的延长线与BC的延长线交于点P.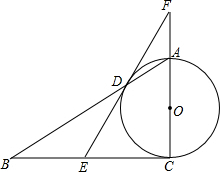 如图,在Rt△ABC中,以直角边AC为直径作⊙O与斜边AB交于点D,点E在BC边上,BE=CE.
如图,在Rt△ABC中,以直角边AC为直径作⊙O与斜边AB交于点D,点E在BC边上,BE=CE.