题目内容
5.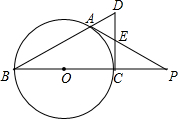 如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD得中点E,AE的延长线与BC的延长线交于点P.
如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA的延长线于点D,取CD得中点E,AE的延长线与BC的延长线交于点P.(1)求证:AP是⊙O的切线;
(2)若tanB=$\frac{1}{2}$,BC=6,求CP的长.
分析 (1)连接AO,AC(如图).欲证AP是⊙O的切线,只需证明OA⊥AP即可;
(2)由CD是⊙O的切线,得到CD⊥OC,根据tanB=$\frac{1}{2}$,得到$\frac{AC}{AB}$=$\frac{1}{2}$根据相似三角形的性质得到$\frac{AP}{PB}=\frac{AC}{AB}$=$\frac{1}{2}$,得到PA=2PC,根据相似三角形的性质解方程即可得到结论.
解答 (1)证明:连接AO,AC(如图).
∵BC是⊙O的直径,
∴∠BAC=∠CAD=90°.
∵E是CD的中点,
∴CE=DE=AE.
∴∠ECA=∠EAC.
∵OA=OC,
∴∠OAC=∠OCA.
∵CD是⊙O的切线,
∴CD⊥OC.
∴∠ECA+∠OCA=90°.
∴∠EAC+∠OAC=90°.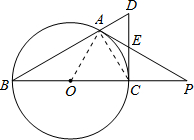
∴OA⊥AP.
∵A是⊙O上一点,
∴AP是⊙O的切线;
(2)解:∵tanB=$\frac{1}{2}$,
∴$\frac{AC}{AB}$=$\frac{1}{2}$,
∵AP是⊙O的切线;
∴∠B=∠CAP,∵∠P=∠P,
∴△APC∽△BPA,
∴$\frac{AP}{PB}=\frac{AC}{AB}$=$\frac{1}{2}$,
∴PA=2PC,
∵△APC∽△BPA,
∴$\frac{PA}{PB}=\frac{PC}{PA}$,
∴PA2=PC•PB,
即(2PC)2=(PC+6)•PC,
∴PC=2.
点评 本题考查了切线的判定和性质,相似三角形的判定和性质,圆周角定理正确的作出辅助线是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
15.下列运算正确的是( )
| A. | 2a2+a3=2a5 | B. | 2a2•a3=2a6 | C. | (-2a2)3=-8a5 | D. | (-2a3)2=4a6 |
16.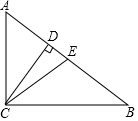 如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )
如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )
 如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )
如图,在Rt△ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为( )| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 6 | D. | 6$\sqrt{3}$ |
10.已知5x=m,5y=n,则52x+3y等于( )
| A. | 2m+3n | B. | m2+n2 | C. | 6mn | D. | m2n3 |
17. 已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )
已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )
 已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )
已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )| A. | x<0 | B. | x>0 | C. | x<2 | D. | x>2 |
14.正多边形的中心角是30°,那么这个正多边形的边数是( )
| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
15.一元二次方程x2-2x=0根的判别式的值为( )
| A. | 4 | B. | 2 | C. | 0 | D. | -4 |
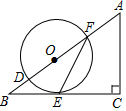 如图,在△ABC中,∠C=90°,D,F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,∠OFE=$\frac{1}{2}$∠A.
如图,在△ABC中,∠C=90°,D,F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,∠OFE=$\frac{1}{2}$∠A.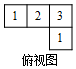 由7个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则其左视图是( )
由7个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则其左视图是( )