题目内容
2. 如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )
如图,大三角形与小三角形是位似图形.若小三角形一个顶点的坐标为(m,n),则大三角形中与之对应的顶点坐标为( )| A. | (-2m,-2n) | B. | (2m,2n) | C. | (-2n,-2m) | D. | (2n,2m) |
分析 过C作CR⊥X轴于R,CK⊥Y轴于K,过F作FG⊥X轴于G,FH⊥Y轴于H,根据中心对称图形的性质和位似图形性质得出$\frac{OB}{OE}$=$\frac{OA}{OD}$=$\frac{1}{2}$,根据平行线分线段成比例定理得到$\frac{OC}{OF}$=$\frac{OR}{OG}$=$\frac{CK}{FH}$=$\frac{1}{2}$,把(m,n)代入即可求出答案.
解答  解:过C作CR⊥X轴于R,CK⊥Y轴于K,过F作FG⊥X轴于G,FH⊥Y轴
解:过C作CR⊥X轴于R,CK⊥Y轴于K,过F作FG⊥X轴于G,FH⊥Y轴
根据图象得:$\frac{OA}{OD}$=$\frac{1}{2}$,
∵大三角形与小三角形是位似图形,
∴$\frac{OB}{OE}$=$\frac{OA}{OD}$=$\frac{OC}{OF}$=$\frac{1}{2}$,
根据平行线分线段成比例定理得:$\frac{OC}{OF}$=$\frac{OR}{OG}$=$\frac{CK}{FH}$=$\frac{1}{2}$,
∵CR=OK=-n,CK=OR=-m,
∴FH=OG=-2m,FG=-2n,
∴小三角形上的顶点(m,n)对应于大三角形上的顶点是(-2m,-2n),
故选A.
点评 本题主要考查对位似变换,平行线分线段成比例定理,关于原点对称的点的坐标等知识点的理解和掌握,能熟练地利用性质进行计算是解此题的关键.

练习册系列答案
相关题目
12. 如图AB∥DE,∠ABC=30°,∠BCD=80°,则∠CDE=( )
如图AB∥DE,∠ABC=30°,∠BCD=80°,则∠CDE=( )
 如图AB∥DE,∠ABC=30°,∠BCD=80°,则∠CDE=( )
如图AB∥DE,∠ABC=30°,∠BCD=80°,则∠CDE=( )| A. | 20° | B. | 50° | C. | 60° | D. | 100° |
10.已知5x=m,5y=n,则52x+3y等于( )
| A. | 2m+3n | B. | m2+n2 | C. | 6mn | D. | m2n3 |
17. 已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )
已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )
 已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )
已知一次函数y=kx+b(k≠0)的图象如图所示,则不等式kx+b>1的解集为( )| A. | x<0 | B. | x>0 | C. | x<2 | D. | x>2 |
7.已知某圆锥的底面半径为3cm,母线长5cm,则它的侧面展开图的面积为( )
| A. | 30cm2 | B. | 15cm2 | C. | 30πcm2 | D. | 15πcm2 |
14.正多边形的中心角是30°,那么这个正多边形的边数是( )
| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
11. 实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
 实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )| A. | ac>bc | B. | |a-b|=a-b | C. | -a<-b | D. | a-c<b-c |
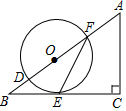 如图,在△ABC中,∠C=90°,D,F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,∠OFE=$\frac{1}{2}$∠A.
如图,在△ABC中,∠C=90°,D,F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,∠OFE=$\frac{1}{2}$∠A. 如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.