题目内容
18.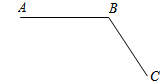 如图,平面上有A、B、C三点.
如图,平面上有A、B、C三点.(1)经过A、B、C三点画⊙O;(保留画图痕迹,不写画法)
(2)如果∠OBA=45°,∠OBC=60°,AB=4cm,求⊙O的半径和BC的长.
分析 (1)分别作AB和BC的垂直平分线,它们的交点为点O,然后以O点为圆心,OB为半径作圆即可;
(2)连结OB,AB的垂直平分线交AB于D,BC的垂直平分线交BC于E,则DB=$\frac{1}{2}$AB=2,BE=$\frac{1}{2}$BC,先在Rt△ODB中,由∠OBD=45°可得OB=$\sqrt{2}$BD=2$\sqrt{2}$,然后在Rt△OBE中利用∠OBC的余弦可求出BE,从而得到BC的长.
解答 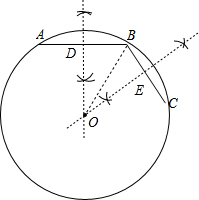 解:(1)如图;
解:(1)如图;
(2)连结OB,AB的垂直平分线交AB于D,BC的垂直平分线交BC于E,
∵OD垂直平分AB,
∴DB=$\frac{1}{2}$AB=2,
在Rt△ODB中,∵∠OBD=45°,
∴OB=$\sqrt{2}$BD=2$\sqrt{2}$,
∵OE垂直平分BC,
∴BE=$\frac{1}{2}$BC,
在Rt△OBE中,∵∠OBC=60°,
∴BE=OBcos60°=2$\sqrt{2}$×$\frac{1}{2}$=$\sqrt{2}$,
∴BC=2BE=2$\sqrt{2}$,
即⊙O的半径为2$\sqrt{2}$和BC的长为2$\sqrt{2}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了三角形的外接圆与外心.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
3.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.5}$ | C. | $\sqrt{4}$ | D. | $\sqrt{6}$ |
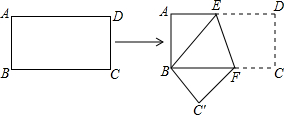
 如图,已知△ABC中,∠ACB=90°,CE是中线,△ACD与△ACE关于直线AC对称.
如图,已知△ABC中,∠ACB=90°,CE是中线,△ACD与△ACE关于直线AC对称.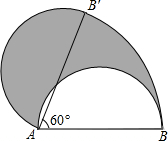 如图,直径AB为6的半圆,绕点A逆时针旋转60°此时点B到达点B′,求圆中阴影部分的面积.
如图,直径AB为6的半圆,绕点A逆时针旋转60°此时点B到达点B′,求圆中阴影部分的面积.