题目内容
13.如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.求:(1)折叠后DE的长;
(2)以折痕EF为边的正方形面积.
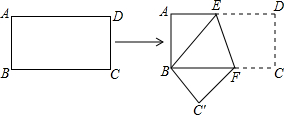
分析 (1)设DE长为xcm,则AE=(9-x)cm,BE=xcm,根据勾股定理得出AE2+AB2=BE2,即(9-x)2+32=x2,解方程求出x,即可得出DE的长;
(2)连接BD,作EG⊥BC于G,则四边形ABGE是矩形,∠EGF=90°,得出EG=AB=3,BG=AE=4,得出GF=1,由勾股定理求出EF2,即可得出以EF为边的正方形面积.
解答 解:(1)设DE长为xcm,则AE=(9-x)cm,BE=xcm,
∵四边形ABCD是矩形,
∴∠A=90°,
根据勾股定理得:AE2+AB2=BE2,
即(9-x)2+32=x2,
解得:x=5,
即DE长为5cm,
(2)作EG⊥BC于G,如图所示: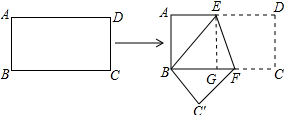
则四边形ABGE是矩形,∠EGF=90°,
∴EG=AB=3,BG=AE=4,
∴GF=1,
∴EF2=EG2+GF2=32+12=10,
∴以EF为边的正方形面积为EF2=10cm2.
点评 本题考查了矩形的性质、翻折变换、勾股定理以及正方形的面积;熟练掌握矩形和翻折变换的性质,运用勾股定理进行计算是解决问题的关键.

练习册系列答案
相关题目
12.某商场推销某一运动服,先做了市场调查,得到销售量y(件)于每件售出价格x(元)的关系如下表.
(1)求y与x的函数关系式;
(2)若物价部门规定该商品的价格不能高于60元,且不能低于45元,商场将售价定为多少时,该商品的销量最大?
| 售出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量y(件) | 500 | 490 | 480 | 470 | … |
(2)若物价部门规定该商品的价格不能高于60元,且不能低于45元,商场将售价定为多少时,该商品的销量最大?
1.已知:Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,设△ABC的面积为s、周长为l.
(1)填表:
(2)仔细观察表中你填写的数据反映出来的规律,如果a、b、c为已知的正实数,且设a+b-c=m,那么可猜想$\frac{s}{l}$=$\frac{m}{4}$.(用含m的代数式表示)
(3)证明你的猜想.
(1)填表:
| a | b | c | a+b-c | $\frac{s}{l}$ |
| 3 | 4 | 5 | 2 | $\frac{1}{2}$ |
| 5 | 12 | 13 | 4 | 1 |
| 8 | 15 | 17 | 6 | $\frac{3}{2}$ |
(3)证明你的猜想.
5.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8a}$ | B. | $\sqrt{5a}$ | C. | $\sqrt{0.5x}$ | D. | $\sqrt{{a}^{2}+{a}^{2}b}$ |
2.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{14}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{4}$ |
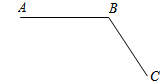 如图,平面上有A、B、C三点.
如图,平面上有A、B、C三点.