题目内容
6.如图,已知正方形ABCD的边长为40cm,E为AD边的中点,G为BC的延长线上一点,连结EG交CD于点F.(1)若FE=FC,求FC的长;
(2)在(1)的条件下,现有一动点P,从A点出发,以5cm/s的速度沿A→E→F→C的路线运动,过点P作PM⊥AB于M,PN⊥BC于N.
①当t为何值时,矩形PMBN恰好是一个正方形?
②若设矩形PMBN的面积为S,试求S与t之间的函数关系式,并写出自变量t的取值范围;
③在点P从A点运动到C点的整个过程中,试问是否存在这样的t的值,使得矩形PMBN的面积恰为888?若存在,求出t的值;若不存在,请说明理由.
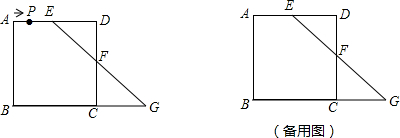
分析 (1)设FC=xcm,则EF=FC=xcm,DF=(40-x)cm,在直角△DEF中,利用勾股定理即可列方程求解;
(2)①以BC所在直线为x轴,AB所在直线为y轴建立坐标系,求得直线EF的解析式,根据P的横纵坐标相等即可求解;
②分成0<t≤4,4<t≤9,9<t≤$\frac{65}{4}$三种情况进行讨论,利用矩形的面积公式以及相似三角形的性质即可求解;
③根据②的结果列方程求解即可.
解答  解:(1)设FC=xcm,则EF=FC=xcm,DF=(40-x)cm.
解:(1)设FC=xcm,则EF=FC=xcm,DF=(40-x)cm.
在直角△DEF中,DE2+DF2=EF2,
则202+(40-x)2=x2,
解得:x=25,
则FC=25cm;
(2)①当P在AE上和FC上时,矩形PMBN不是正方形.
当P在EF上时,如图(1),如图建立坐标系,则E的坐标是(20,40),F的坐标是(40,25).
设EF的解析式是y=kx+b,
则$\left\{\begin{array}{l}{20k+b=40}\\{40k+b=25}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=55}\end{array}\right.$,
则直线EF的解析式是:y=-$\frac{3}{4}$x+55,
设P的坐标是(m,m),
代入y=-$\frac{3}{4}$x+55中得:m=-$\frac{3}{4}$m+55,
解得:m=$\frac{220}{7}$
则P的坐标是($\frac{220}{7}$,$\frac{220}{7}$);
则PE=$\sqrt{(\frac{220}{7}-20)^{2}+(\frac{220}{7}-40)^{2}}$=$\frac{100}{7}$.
则t=(20+$\frac{100}{7}$)÷5=$\frac{48}{7}$(s);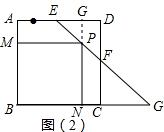
②当0<t≤4时,S=40t;
当4<t≤9时,P在EF上,如图(2),则PE=5t-20,作PG⊥AD于点G,
则△EGP∽△EDF,
则$\frac{GP}{DF}=\frac{EP}{EF}$=$\frac{EG}{ED}$,
∵直角△DEF中,EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\sqrt{2{0}^{2}+1{5}^{2}}$=25,
∴$\frac{GP}{15}$=$\frac{5t-20}{25}$=$\frac{EG}{20}$,
解得:GP=3t-12,EG=4t-16.
∴PN=40-GP=40-(3t-12)=52-3t,PM=40-DG=AE+EG=20+4t-16=4+4t,
则S=(52-3t)(4+4t)=-12t2+200t+208;
当9<t≤$\frac{65}{4}$时,P在FC上,N与C重合,PM=40,PN=5t-20-25=5t-45.
则S=40(5t-45)=200t-180.
即S=$\left\{\begin{array}{l}{40t(t≤4)}\\{-12{t}^{2}+200t+208(4<t≤9)}\\{200t-180(9<t≤\frac{65}{4})}\end{array}\right.$;
(3)当0<t≤4时,S的最大值是40×4=160<888.
当4<t≤9时,-12t2+200t+208=888,即3t2-50t+85=0,
解得:t1=$\frac{25+\sqrt{370}}{3}$(舍去),t2=$\frac{25-\sqrt{370}}{3}$.
则t=$\frac{25-\sqrt{370}}{3}$.
当9<t≤$\frac{65}{4}$时,200t-180=888,
解得:t=$\frac{267}{50}$<9(舍去).
总之,当t=$\frac{25-\sqrt{370}}{3}$时,S恰好是888.
点评 本题考查了正方形的性质和相似三角形的判定与性质以及勾股定理的应用,正确进行讨论是解决本题的关键.

 学业测评一课一测系列答案
学业测评一课一测系列答案(1)填表:
| a | b | c | a+b-c | $\frac{s}{l}$ |
| 3 | 4 | 5 | 2 | $\frac{1}{2}$ |
| 5 | 12 | 13 | 4 | 1 |
| 8 | 15 | 17 | 6 | $\frac{3}{2}$ |
(3)证明你的猜想.
| A. | $\sqrt{\frac{1}{2}x}$ | B. | $\sqrt{18x}$ | C. | $\sqrt{3x}$ | D. | $\sqrt{{x}^{2}y}$ |
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: 如图,平面上有A、B、C三点.
如图,平面上有A、B、C三点. 一次函数y=$\frac{3}{2}$x-3
一次函数y=$\frac{3}{2}$x-3