题目内容
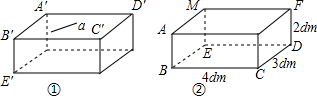
2.小敏将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°,感觉最舒适(如图1),侧面示意图为图2.使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O′C⊥OA于点C,O′C=12cm.(1)求∠CAO′的度数;
(2)显示屏的顶部B′比原来升高了多少?

分析 (1)通过解直角三角形即可得到结果;
(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD的长,由C、O′、B′三点共线可得结果,计算O′B′+O′C-BD即可求解.
解答 解:(1)∵O′C⊥OA于C,OA=OB=24cm,
∴sin∠CAO′=$\frac{O'C}{O'A}=\frac{O'C}{OA}=\frac{1}{2}$,
∴∠CAO′=30°.
(2)过点B作BD⊥AO交AO的延长线于D.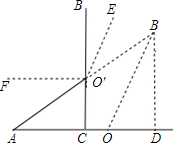
∵sin∠BOD=$\frac{BD}{OB}$,
∴BD=OB•sin∠BOD,
∵∠AOB=120°,
∴∠BOD=60°,
∴BD=OB•sin∠BOD=24×$\frac{{\sqrt{3}}}{2}=12\sqrt{3}$.
∵O′C⊥OA,∠CAO′=30°,
∴∠AO′C=60°.
∵∠AO′B′=120°,
∴∠AO′B′+∠AO′C=180°.
∴O′B′+O′C-BD=24+12-$12\sqrt{3}$=36-$12\sqrt{3}$.
∴显示屏的顶部B′比原来升高了(36-$12\sqrt{3}$)cm.
点评 本题考查了解直角三角形的应用,旋转的性质,正确的画出图形是解题的关键.

练习册系列答案
相关题目
13.某学校组织了一次知识竞赛,初二年级、初三年级各10名选手的比赛成绩如下(本次竞赛满分10分):
(1)初二成绩的中位数是9.5分,初三成绩的众数是10分;
(2)运用学过的数学知识说明、判断,哪个年级选手的成绩整体比较稳定.
| 初二 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 初三 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)运用学过的数学知识说明、判断,哪个年级选手的成绩整体比较稳定.
17. 将一副直角三角尺按如图所示摆放,则图中锐角∠α的度数是( )
将一副直角三角尺按如图所示摆放,则图中锐角∠α的度数是( )
 将一副直角三角尺按如图所示摆放,则图中锐角∠α的度数是( )
将一副直角三角尺按如图所示摆放,则图中锐角∠α的度数是( )| A. | 45° | B. | 60° | C. | 70° | D. | 75° |
 AB是⊙O的直径,弦CD垂直平分半径OA,若CD长为6,则⊙O的半径长为2$\sqrt{3}$.
AB是⊙O的直径,弦CD垂直平分半径OA,若CD长为6,则⊙O的半径长为2$\sqrt{3}$.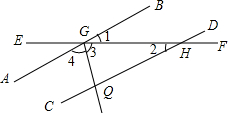 如图,直线AB,CD被直线EF所截,∠AGH的平分线交CD于点Q,已知∠1=∠2=$\frac{1}{4}$∠3,求∠1,∠3的度数.
如图,直线AB,CD被直线EF所截,∠AGH的平分线交CD于点Q,已知∠1=∠2=$\frac{1}{4}$∠3,求∠1,∠3的度数.