题目内容
17．
将一副直角三角尺按如图所示摆放，则图中锐角∠α的度数是（ ）| A． | 45° | B． | 60° | C． | 70° | D． | 75° |
分析 根据直角三角板∠1=60°，∠3=45°，∠BAC=90°，再根据角的和差关系可得∠2的度数，再利用三角形内角和为180°计算出∠α的度数．
解答 
解：根据直角三角板∠1=60°，∠3=45°，∠BAC=90°，
∵∠2+∠3=90°，
∴∠2=90°-45°=45°，
∴∠α=180°-45°-60°=75°，
故选：D．
点评 此题主要考查了三角形内角和定理，以及角的计算，关键是掌握三角形内角和为180°，正确计算出∠2的度数．
练习册系列答案
相关题目
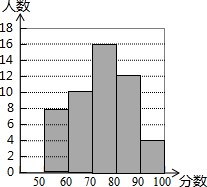本学期初，我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价，评价小组从八年级学生中选取部分学生针对“信息素养”进行测试，并将测试结果绘制成如下统计图（如图）．根据图中信息，解答下列问题：
在矩形ABCD中，E、F、M分别为AB、BC、CD边上的点，且AB=6，BC=7，AE=3，DM=2，EF⊥FM，则EM的长为5$\sqrt{2}$．
5．
如图，在△ABC中，点D在BC上，∠DAC=∠B，BD=4，DC=5，DE∥AC交AB于点E，则DE的长为（ ）
如图，在△ABC中，点D在BC上，∠DAC=∠B，BD=4，DC=5，DE∥AC交AB于点E，则DE的长为（ ）| A． | $\sqrt{5}$ | B． | $\frac{4\sqrt{5}}{3}$ | C． | 3 | D． | 4 |
12．
如图，O是直线AB上的一点，∠BOC=120°，OD平分∠AOC.0E平分∠BOC，则图中与∠BOE互余的角有（ ）
如图，O是直线AB上的一点，∠BOC=120°，OD平分∠AOC.0E平分∠BOC，则图中与∠BOE互余的角有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
比较图中以A为一个端点的线段的大小，并把它们用“＜”号连接起来．
如图，已知∠ACD=∠BCE，AC=DC，如果要得到△ACB≌△DCE，那么还需要添加的条件是∠A=∠D．（填写一个即可，不得添加辅助线和字母）