题目内容
12.计算:(1)-22×3-(-3×2)3
(2)[-$\frac{7}{12}$+$\frac{3}{4}$-$\frac{5}{6}$-(-$\frac{5}{18}$)]×(-36)
(3)先化简,再求值:(5a2-3b2)-3(a2-b2)-(-b2).其中a=3,b=-2.
(4)化简:己知A=-3m2-4m+1,B=2m2+6m-12,求:2A-3B.
分析 (1)根据有理数的加、减、乘、除、乘方进行计算即可;
(2)根据乘法的分配律进行计算即可;
(3)先去括号,再合并同类项,代入a,b的值计算即可;
(4)将A,B的值代入2A-3B计算即可.
解答 解:(1)原式=-12-(-6)×(-6)×(-6)
=-12+216=204;
(2)解:原式=(-$\frac{7}{12}$)×(-36)+$\frac{3}{4}$×(-36)-$\frac{5}{6}$×(-36)-(-$\frac{5}{18}$)×(-36)
=21-27+30-10
=14;
(3)原式=5a2-3b2-3a2+3b2+b2
=2a2+b2,
当a=3,b=-2时,原式=2×32+(-2)2
=2×9+4
=22;
(4)∵A=-3m2-4m+1,B=2m2+6m-12,
∴2A-3B=2(-3m2-4m+1)-3(2m2+6m-12),
=-6m2-8m+2-6m2-18m+36
=-12m2-26m+38.
点评 本题考查了有理数的混合运算以及整式的加减,掌握乘法的分配律,整式混合运算的运算顺序是解题的关键.

练习册系列答案
相关题目
20. 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2-4c<0;
②b+c=0;
③2b+c<-2;
④当x>3时,x2+(b-1)x+c<0.
其中正确的个数为( )
 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c<0;
②b+c=0;
③2b+c<-2;
④当x>3时,x2+(b-1)x+c<0.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17. 如图,直线OA过点(4,3),则tanα=( )
如图,直线OA过点(4,3),则tanα=( )
 如图,直线OA过点(4,3),则tanα=( )
如图,直线OA过点(4,3),则tanα=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
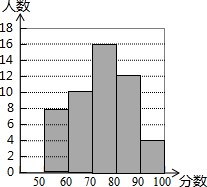 本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题: 如图,点A在第一象限,以点A为顶点的抛物线经过原点,与x轴的正半轴交于点B,对称轴为x=1,点C在抛物线上,且位于点A,O之间(点C与A,O不重合),若△AOC的周长为m,则四边形ACOB的周长为( )
如图,点A在第一象限,以点A为顶点的抛物线经过原点,与x轴的正半轴交于点B,对称轴为x=1,点C在抛物线上,且位于点A,O之间(点C与A,O不重合),若△AOC的周长为m,则四边形ACOB的周长为( )