题目内容
3.已知二次函数y=x2-2x+k的图象经过点A(1,y1),B(-$\sqrt{2}$,y2),C(-2,y3),则y1,y2,y3大小关系是y2>y3>y1.(用“<”、“>”或“=”连接)分析 根据函数解析式的特点,其对称轴为x=1,图象开口向上;在对称轴的左侧,利用y随x的增大而减小,可判断y3<y2,根据二次函数图象的对称性可判断y2>y1;于是y2>y3>y1.
解答 解:根据二次函数图象的对称性可知,其对称轴为x=1,B(-$\sqrt{2}$,y2),C(-2,y3),在对称轴的左侧,y随x的增大而减小,
因为-2<-$\sqrt{2}$,于是y2>y3,
因为x=1时有最小值所以y1最小,
故答案为:y2>y3>y1.
点评 本题考查了函数图象上的点的坐标与函数解析式的关系,同时考查了函数的对称性及增减性.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
14.若圆的一条弦把圆分成度数比为1:3的两条弧,则该弦所对的圆心角度数是( )
| A. | 90° | B. | 45° | C. | 135° | D. | 45°或135° |
11.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A($\frac{3}{2}$,0),B(0,2),则点B6的坐标为( )
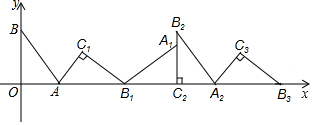

| A. | (18,0) | B. | (18,2) | C. | (16,2) | D. | (16,0) |
15.在平面直角坐标系中,平移二次函数y=(x-2015)(x-2017)+3的图象,使其与x轴两交点间的距离为2个单位长度,则下列平移方式中可实现上述要求的是( )
| A. | 向上平移3个单位 | B. | 向下平移3个单位 | C. | 向左平移3个单位 | D. | 向右平移3个单位 |
 已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.
已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F. 在△ABC中,∠C=90°,∠ABC的平分线BD与AC交于D点,若CD=2,则点D到AB的距离是2.
在△ABC中,∠C=90°,∠ABC的平分线BD与AC交于D点,若CD=2,则点D到AB的距离是2. 如图,用一个半径为30cm扇形铁皮,制作一个无底的圆锥(不计损耗),经测量圆锥的底面半径r为10cm,则扇形铁皮的面积为300πcm2.(结果保留π)
如图,用一个半径为30cm扇形铁皮,制作一个无底的圆锥(不计损耗),经测量圆锥的底面半径r为10cm,则扇形铁皮的面积为300πcm2.(结果保留π)