题目内容
19.从-6,-5,…,0,1,2,3,4,5这12个数中,随机抽取一个数,记为a,若数a使关于x的方程$\frac{x}{x-3}$-$\frac{1-a}{3-x}$=-1有整数解,那么这12个数中所有满足条件的数a的值之和是( )| A. | 10 | B. | -8 | C. | -6 | D. | -10 |
分析 先解关于x的方程$\frac{x}{x-3}$-$\frac{1-a}{3-x}$=-1,得到x=$\frac{2+a}{2}$,再根据方程$\frac{x}{x-3}$-$\frac{1-a}{3-x}$=-1有整数解,即可得到a的取值,进而得出所有满足条件的数a的值之和.
解答 解:关于x的方程$\frac{x}{x-3}$-$\frac{1-a}{3-x}$=-1,去分母可得x+1-a=3-x,
∴x=$\frac{2+a}{2}$,
∵方程$\frac{x}{x-3}$-$\frac{1-a}{3-x}$=-1有整数解,
∴2+a能被2整除,且$\frac{2+a}{2}$≠3,
∴a≠4,
∴在12个数中,符合题意的有:-6,-4,-2,0,2,
∴满足条件的数a的值之和是-10,
故选:D.
点评 本题主要考查了分式方程的解,解题时注意:在解方程的过程中,因为在把分式方程化为整式方程时,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.

练习册系列答案
相关题目
9.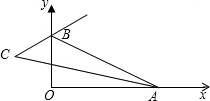 如图,在平面直角坐标系中,A、B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A、B运动的变化情况正确的是( )
如图,在平面直角坐标系中,A、B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A、B运动的变化情况正确的是( )
 如图,在平面直角坐标系中,A、B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A、B运动的变化情况正确的是( )
如图,在平面直角坐标系中,A、B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A、B运动的变化情况正确的是( )| A. | 点B不动,在点A向右运动的过程中,∠C的度数逐渐减小 | |
| B. | 点A不动,在点B向上运动的过程中,∠C的度数逐渐减小 | |
| C. | 在点A向左运动,点B向下运动的过程中,∠C的度数逐渐增大 | |
| D. | 在点A、B运动的过程中,∠C的度数不变 |
7.一次函数y=-5x-1的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |