题目内容
10.已知关于x、y的方程组$\left\{\begin{array}{l}{x+y=1-a}\\{x-y=3a+5}\end{array}\right.$给出下列结论:①当a=1时,方程组的解也是方程x-y=3的解;②当x与y互为相反数时,a=1;③不论a取什么实数,2x+y的值始终不变,正确的是②③(把正确答案的序号全部都填上).分析 根据题目中的条件代入原来的方程组中,即可判断结论是否成立,从而可以解答本题.
解答 解:当a=1时,$\left\{\begin{array}{l}{x+y=0}\\{x-y=8}\end{array}\right.$,得$\left\{\begin{array}{l}{x=4}\\{y=-4}\end{array}\right.$,则x-y=4-(-4)=8,∴①中的结论是错的,
当x与y互为相反数时,0=1-a,得a=1,故②中的结论是正确的,
∵$\left\{\begin{array}{l}{x+y=1-a}\\{x-y=3a+5}\end{array}\right.$,得$\left\{\begin{array}{l}{x=3+a}\\{y=-2-2a}\end{array}\right.$,则2x+y=2(3+a)+(-2-2a)=4,故③中的结论正确,
故答案为:②③.
点评 本题考查二元一次方程组的解、二元一次方程的解,解答本题的关键是明确题意,可以判断题目中的各个结论是否成立.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
14.已知平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为( )
| A. | (-3,4) | B. | (4,-3) | C. | (3,-4) | D. | (-4,3) |
19.从-6,-5,…,0,1,2,3,4,5这12个数中,随机抽取一个数,记为a,若数a使关于x的方程$\frac{x}{x-3}$-$\frac{1-a}{3-x}$=-1有整数解,那么这12个数中所有满足条件的数a的值之和是( )
| A. | 10 | B. | -8 | C. | -6 | D. | -10 |
20.把△ABC经过平移后得到△A′B′C′,已知A(4,3),B(3,1),B′(1,-1),C′(2,0),则△ABC的面积为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
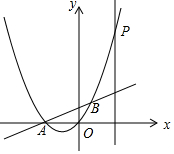 如图,抛物线y=x2+2x与直线y=$\frac{1}{2}$x+1交于A、B两点,与直线x=2交于点P,将抛物线沿着射线AB平移$\frac{3}{2}\sqrt{5}$个单位.
如图,抛物线y=x2+2x与直线y=$\frac{1}{2}$x+1交于A、B两点,与直线x=2交于点P,将抛物线沿着射线AB平移$\frac{3}{2}\sqrt{5}$个单位.
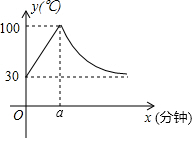 教室内的饮水机接通电源进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(分钟)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为30℃时,接通电源后,水温y(℃)和时间x(分钟)的关系如图.
教室内的饮水机接通电源进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(分钟)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为30℃时,接通电源后,水温y(℃)和时间x(分钟)的关系如图.