题目内容
16.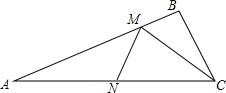 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3 |
分析 作C关于AB的对称点E,过E作EN⊥AC于N,连接AE,则EN=CM+MN的最小值,由对称的性质得到AB垂直平分BC,推出△AEN是等腰直角三角形,解直角三角形即可得到结论.
解答  解:作C关于AB的对称点E,过E作EN⊥AC于N,连接AE,
解:作C关于AB的对称点E,过E作EN⊥AC于N,连接AE,
则EN=CM+MN的最小值,
由对称的性质得:AB垂直平分BC,
∴AE=AC=6,∠EAC=2∠BAC=45°,
∴△AEN是等腰直角三角形,
∴EN=$\frac{\sqrt{2}}{2}$AE=3$\sqrt{2}$,
故选C.
点评 本题考查的是轴对称-最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过线段平分线性质,垂线段最短,确定线段和的最小值.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
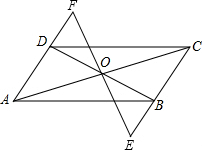 如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么?
如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么? 如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.
如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.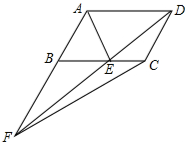 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.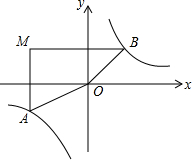 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{2}{x}$的图象交于A、B两点,则四边形MAOB的面积为8.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{2}{x}$的图象交于A、B两点,则四边形MAOB的面积为8. 已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.
已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.