题目内容
19.先化简,再求值:($\frac{1}{x-3}$-$\frac{x+1}{{x}^{2}-1}$)•(x-3),从不大于4的正整数中,选择一个合适的值代入x求值.分析 先根据分式混合运算的法则把原式进行化简,再选出合适的x的值代入进行计算即可.
解答 解:原式=[$\frac{1}{x-3}$-$\frac{1}{x-1}$]•(x-3)
=$\frac{x-1-x+3}{(x-3)(x-1)}$•(x-3)
=$\frac{2}{x-1}$,
当x=4时,原式=$\frac{2}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
11.某市努力改善空气质量,近年来空气质量明显好转,根据该市环境保护局公布的2010-2014这五年各年全年空气质量优良的天数如表所示,根据表中信息回答:
(1)这五年的全年空气质量优良天数的中位数是245,平均数是243;
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是2012年(填写年份);
(3)求这五年的全年空气质量优良天数的方差.
| 2010 | 2011 | 2012 | 2013 | 2014 |
| 234 | 233 | 245 | 247 | 256 |
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是2012年(填写年份);
(3)求这五年的全年空气质量优良天数的方差.
 如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E. 如图,将一相邻两边长比为2:3的矩形纸片ABCD沿对角线BD进行翻折,点A落在点E处,连接CE,则CE:BD为5:13.
如图,将一相邻两边长比为2:3的矩形纸片ABCD沿对角线BD进行翻折,点A落在点E处,连接CE,则CE:BD为5:13.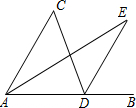 如图,点B是AD延长线上的一点,DE∥AC,AE平分∠CAB,∠C=50°,∠E=30°,则∠CDA的度数等于70°.
如图,点B是AD延长线上的一点,DE∥AC,AE平分∠CAB,∠C=50°,∠E=30°,则∠CDA的度数等于70°. 如图,PM⊥OA于M,PN⊥OB于N,PM=PN,∠AOC=25°,则∠AOB的度数是50°.
如图,PM⊥OA于M,PN⊥OB于N,PM=PN,∠AOC=25°,则∠AOB的度数是50°.