题目内容
8．
如图，PM⊥OA于M，PN⊥OB于N，PM=PN，∠AOC=25°，则∠AOB的度数是50°．
分析 由PM⊥OA，PN⊥OB，PM=PN，可判定OC是∠AOB的角平分线，继而求得答案．
解答 解：∵PM⊥OA，PN⊥OB，PM=PN，
∴OC是∠AOB的角平分线，
∴∠AOB=2∠AOC=50°．
故答案为：50°．
点评 此题考查了角平分线的性质．此题比较简单，注意数形结合思想的应用．
练习册系列答案
相关题目
16．2014年2月15日山西晚报报道，为了加强学生体育锻炼，根据太原市教育局安排，2014年将继续大力开展阳光体育运动，切实保证中小学生每天一小时校园体育活动时间．该市的教育部门为了了解该市中学生参加校园体育活动的情况．对某中学部分学生参加校园体育活动的时间x（h）进行抽样调查，将调查结果分成了A、B、C、D、E五个组，并利用所得数据绘制了如图1、如图2所示的两幅不完整的统计图． 
根据统计图表提供的信息，解答下列问题：
（1）该抽样调查的样本容量为80，并补全频数分布直方图；
（2）若该中学共有2200名学生，请估计全校共有多少名学生参加校园体育活动的时间大于等于1.5h．
（3）该中学学生进行校园体育活动时的项目有篮球、羽毛球和跳绳．在所调查的学生中，有26名学生在玩篮球，30名学生在打羽毛球，若将打羽毛球和跳绳的学生分别进行分组，所分的组数相同，但每组打羽毛球的人数比跳绳的人数多1人，小权在羽毛球的某一小组中，该小组要选出一个组长，求小权当选组长的概率．
| 组别 | 活动时间x/h |
| A | 0≤x＜0.5 |
| B | 0.5≤x＜1 |
| C | 1≤x＜1.5 |
| D | 1.5≤x＜2 |
| E | 2≤x＜2.5 |
（1）该抽样调查的样本容量为80，并补全频数分布直方图；
（2）若该中学共有2200名学生，请估计全校共有多少名学生参加校园体育活动的时间大于等于1.5h．
（3）该中学学生进行校园体育活动时的项目有篮球、羽毛球和跳绳．在所调查的学生中，有26名学生在玩篮球，30名学生在打羽毛球，若将打羽毛球和跳绳的学生分别进行分组，所分的组数相同，但每组打羽毛球的人数比跳绳的人数多1人，小权在羽毛球的某一小组中，该小组要选出一个组长，求小权当选组长的概率．
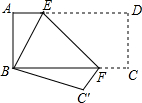如图，将长方形纸片ABCD折叠，使点D与点B重合，点C落在点C'处，折痕为EF．如果∠ABE=20°，那么∠EFB=55度．
如图，AD是△ABC的外角平分线，交BC的延长线于D点，若∠B=30°，∠ACD=100°，求∠DAE的度数．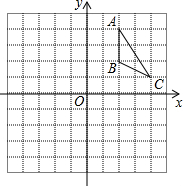
如图，方格纸中的每个小正方形都是边长为1个单位长度的正方形，△ABC的顶点都在格点上，建立平面直角坐标系．
如图，活动课上，小王想要利用所学的数学知识测量某个建筑地所在山坡AE的高度，她先在山脚下的点E处测得山顶A的仰角是30°，然后，她沿着坡度i=1：1的斜坡步行15分钟到达C处，此时，测得点A的俯角是15°．已知小王的步行速度是20米/分，图中点A、B、E、D、C在同一平面内，且点D、E、B在同一水平直线上，求出建筑地所在山坡AE的高度AB．（精确到0.1米，参考数据：$\sqrt{2}$≈1.41）．