题目内容
10.①$\frac{x+4}{0.2}-\frac{x-3}{0.5}≥11$(解集表示在数轴上)②$\left\{{\begin{array}{l}{2({x+3})+5({x-2})<3}\\{\frac{x+1}{3}-1≤\frac{2x+1}{2}}\end{array}}\right.$(解集表示在数轴上)
分析 ①利用不等式的基本性质:先去分母,再去括号,再移项合并同类项,最后系数化1求出不等式的解集;再在数轴上表示出来.
②求出两个不等式的解集,再求出不等式组的公共部分即可.
解答 解:①去分母得,5(x+4)-2(x-3)≥11,
去括号得,5x+20-2x+6≥11,
移项合并同类项得,3x≥-15,
两边同时除以3得,x≥-5.
在数轴上表示为:
②$\left\{\begin{array}{l}{2(x+3)+5(x-2)<3①}\\{\frac{x+1}{3}-1≤\frac{2x+1}{2}②}\end{array}\right.$
解:∵解不等式①得:x<1,
解不等式②得:x≤1,
∴不等式组的解集是x$≥-\frac{7}{4}$,
在数轴上表示为: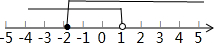 .
.
点评 本题考查了一元一次不等式,一元一次不等式组的应用,解不等式关键不等式的基本性质,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.运用等式性质的变形,正确的是( )
| A. | 如果a=b,那么a+c=b-c | B. | 如果$\frac{a}{c}=\frac{b}{c}$,那么a=b | ||
| C. | 如果a=b,那么$\frac{a}{c}=\frac{b}{c}$ | D. | 如果a=3,那么a2=3a2 |
2.下列计算正确的是( )
| A. | ($\frac{1}{2}$)0=$\frac{1}{2}$ | B. | (-2)-1=$\frac{1}{2}$ | C. | -2×(-5)=10 | D. | 2-3=1 |
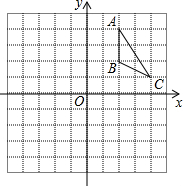 如图,方格纸中的每个小正方形都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
如图,方格纸中的每个小正方形都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.