题目内容
5. 如图,抛物线y=-$\frac{1}{8}{x^2}+\frac{1}{2}$x+4与y轴交于点A、与x轴分别交于B、C两点.
如图,抛物线y=-$\frac{1}{8}{x^2}+\frac{1}{2}$x+4与y轴交于点A、与x轴分别交于B、C两点.(1)求A、B两点坐标;
(2)将Rt△AOB绕点A逆时针旋转90°得到△ADE,求点E的坐标;
(3)求出第一象限内的抛物线上与直线AE距离最远的点的坐标.
分析 (1)分别令x=0,y=0可求得点A、B的坐标;
(2)由点A、B的坐标可求得OA、OB的长,然后由旋转的性质可得到点E的坐标;
(3)延长AE交抛物线与点M,过点P作PN⊥x轴,交直线AE与点N,过点P作PW⊥AE垂足为W.先求得直线AE的解析式,然后求得点M的坐标,设点P(t,-$\frac{1}{8}$t2+$\frac{1}{2}$t+4),则N(t,-t+4),可求得PN=-$\frac{1}{8}$t2+$\frac{3}{2}$t.从而得到△APM的面积与t的函数关系式,利用配方法可求得△APM的最大值,以及此时点P的坐标.
解答 解:(1)∵当x=0时,y=4,
∴A(0,4).
∵当y=0时,-$\frac{1}{8}{x^2}+\frac{1}{2}$x+4=0,
∴x1=-4,x2=8.
∴B(-4,0).
(2)由(1)得OA=OB=4,
∵将△ABO逆时针绕A旋转90°得到△ADE,
∴∠ADE=90°,DE=AD=4.
∴点D(4,4).
∴E(4,0).
(3)如图所示:延长AE交抛物线与点M,过点P作PN⊥x轴,交直线AE与点N,过点P作PW⊥AE垂足为W.
设直线AE的解析式为y=kx+b.
∵将A(0,4),B(,0)代入得:$\left\{\begin{array}{l}{b=4}\\{4k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=}\end{array}\right.$,
∴直线AE的解析式为y=-x+4.
∵将y=-x+4与y=-$\frac{1}{8}{x^2}+\frac{1}{2}$x+4联立解得:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=12}\\{{y}_{2}=-8}\end{array}\right.$,
∴M(12,-8).
设点P(t,-$\frac{1}{8}$t2+$\frac{1}{2}$t+4),则N(t,-t+4),PN=-$\frac{1}{8}$t2+$\frac{1}{2}$t+4-(-t+4)=-$\frac{1}{8}$t2+$\frac{3}{2}$t.
S△APM=$\frac{1}{2}$PN•xM=$\frac{1}{2}$×12×(-$\frac{1}{8}$t2+$\frac{3}{2}$t)=-$\frac{3}{4}$t2+9t=-$\frac{3}{4}$(t-6)2+27.
∴当t=6时,△APM的面积最大.
∴当t=6时,y=-$\frac{1}{8}$×62+$\frac{1}{2}$×6+4=$\frac{5}{2}$.
∴P(6,$\frac{5}{2}$).
∵当△APM面积最大时,PW最大,
∴直线AE最远的点的坐标为P(6,$\frac{5}{2}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了函数解析式与点的坐标的关系、待定系数法求一次函数的解析式、一次函数与二次函数的交点、配方法求二次函数的最值、三角形的面积公式、旋转的性质,列出三角形APM的面积与点P的横坐标t之间的函数关系式是解题的关键.

方案(1)是不改变食品售价,减少总成本;
方案(2)是不改变总成本,提高食品售价.
下面给出的四个图象中虚线表示新的销售方式中利润与销售量的函数图象,则分别反映了方案(1)(2)的图象是( )
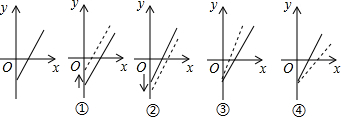
| A. | ②,③ | B. | ①,③ | C. | ①,④ | D. | ④,② |
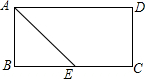 在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )| A. | 2和3 | B. | 3和2 | C. | 4和1 | D. | 1和4 |
| A. |  | B. |  | C. |  | D. |  |
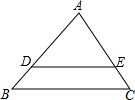 如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )
如图,在△ABC中,D,E分别是AB和AC上的点,满足AD=3,AE=2,EC=1,DE∥BC,则AB=( )| A. | 6 | B. | 4.5 | C. | 2 | D. | 1.5 |
| A. | x-1 | B. | x | C. | $\frac{1}{x}$ | D. | $\frac{1}{x-1}$ |
 如图,在四边形ABCD中,点M、N、P分别是AD、BC、BD的中点,如果$\overrightarrow{BA}=\vec a,\overrightarrow{DC}=\vec b$,那么$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.(用$\vec a和\vec b$表示)
如图,在四边形ABCD中,点M、N、P分别是AD、BC、BD的中点,如果$\overrightarrow{BA}=\vec a,\overrightarrow{DC}=\vec b$,那么$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.(用$\vec a和\vec b$表示)