题目内容
8. 如图,直线AB与CD相交于点O.
如图,直线AB与CD相交于点O.(1)若∠AOD+∠COB=2(∠BOD+∠AOC),求∠AOD,∠BOD的度数.
(2)若∠COB-∠BOD=m°,求∠AOD,∠BOD的度数(用含m°的式子表示)
分析 (1)依据对顶角和领补角的性质求解即可;
(2)结合邻补角的性质以及方程的解答求解即可.
解答 解:(1)∵直线AB与CD相交与点O,
∴∠AOD=∠COB,∠BOD=∠AOC.
∵∠AOD+∠COB=2(∠BOD+∠AOC),
∴∠AOD=2∠BOD.
∵∠AOD+∠BOD=180°,
∴3∠AOD=180°.
∴∠AOD=60°.
∴∠AOD=180°-∠BOD=120°.
(2)∵∠COB+∠BOD=180°,
∴∠COB=180°-∠BOD.
∵∠COB-∠BOD=m°,
∴180°-2∠BOD=m°.
∴∠BOD=90°-$\frac{1}{2}$m°,
∵∠AOD+∠BOD=180°,
∴∠AOD=180°-∠BOD=180°-(90°-$\frac{1}{2}$m°)=90°+$\frac{1}{2}$m°.
点评 本题主要考查的是邻补角和对顶角的性质,掌握相关性质是解题的关键.

练习册系列答案
相关题目
3.某农户共摘收水蜜桃1920千克,为寻求合适的销售价格,进行了6天试销,试销情况如下:
由表中数据可知,试销期间这批水蜜桃的每天销售量y(千克)与售价x(元/千克)之间满足我们曾经学过的某种函数关系.若在这批水蜜桃的后续销售中,每天的销售量y(千克)与售价x(元/千克)之间都满足这一函数关系.
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
①若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
②该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | |
| 售价x(元/千克) | 20 | 18 | 15 | 12 | 10 | 9 |
| 销售量y(千克) | 45 | 50 | 60 | 75 | 90 | 100 |
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
①若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
②该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
20.某公园购进一批平均高度为2m的某种树苗.为了掌握树的生长情况,树苗栽种后,园林工作者对其进行了几年的观测,并记录了每年末这种树的平均高度,如表:
(1)这种树从栽种第几年开始,生长变得缓慢?
(2)栽种后的前4年,每年生长多少米?第5年后每年生长多少米?
(3)请写出栽种后的前4年,树高h1(m)与栽种的时间t(年)之间的函数关系式;
(4)请写出栽种第5年以后,树高h2(m)与栽种后的时间t(年)之间的函数关系式;
(5)这种树按表中的生长速度,求出第11年末树高是多少米?
| 栽后时间/年 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 树高/m | 2.0 | 2.6 | 3.2 | 3.8 | 4.4 | 4.8 | 5.2 | 5.6 | 6.0 | … |
(2)栽种后的前4年,每年生长多少米?第5年后每年生长多少米?
(3)请写出栽种后的前4年,树高h1(m)与栽种的时间t(年)之间的函数关系式;
(4)请写出栽种第5年以后,树高h2(m)与栽种后的时间t(年)之间的函数关系式;
(5)这种树按表中的生长速度,求出第11年末树高是多少米?
18. 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒$\frac{2π}{3}$个单位长度,则2015秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒$\frac{2π}{3}$个单位长度,则2015秒时,点P的坐标是( )
 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒$\frac{2π}{3}$个单位长度,则2015秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒$\frac{2π}{3}$个单位长度,则2015秒时,点P的坐标是( )| A. | (2015,0) | B. | (2015,$\sqrt{3}$) | C. | (2015,-$\sqrt{3}$) | D. | (2016,0) |
 如图是由5个相同的小立方块组成的立体图形,则它的俯视图是( )
如图是由5个相同的小立方块组成的立体图形,则它的俯视图是( )



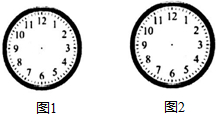 某电视台录制的“奔跑吧兄弟第四季”将在周五21:10播出,此时时钟上的分针与时针所成的角是多少度?在如图中大致标出此时的角(用短箭头、长箭头分别表示时针和分针),并用至少两种方式写出这个角?(可在表盘上标注相应的字母或数字)
某电视台录制的“奔跑吧兄弟第四季”将在周五21:10播出,此时时钟上的分针与时针所成的角是多少度?在如图中大致标出此时的角(用短箭头、长箭头分别表示时针和分针),并用至少两种方式写出这个角?(可在表盘上标注相应的字母或数字)