题目内容
18. 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒$\frac{2π}{3}$个单位长度,则2015秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒$\frac{2π}{3}$个单位长度,则2015秒时,点P的坐标是( )| A. | (2015,0) | B. | (2015,$\sqrt{3}$) | C. | (2015,-$\sqrt{3}$) | D. | (2016,0) |
分析 设第n秒运动到Pn(n为自然数)点,根据点P的运动规律找出部分Pn点的坐标,根据坐标的变化找出变化规律“P4n+1(4n+1,$\sqrt{3}$),P4n+2(4n+2,0),P4n+3(4n+3,-$\sqrt{3}$),P4n+4(4n+4,0)”,依此规律即可得出结论.
解答 解:设第n秒运动到Pn(n为自然数)点,
观察,发现规律:P1(1,$\sqrt{3}$),P2(2,0),P3(3,-$\sqrt{3}$),P4(4,0),P5(5,$\sqrt{3}$),…,
∴P4n+1(4n+1,$\sqrt{3}$),P4n+2(4n+2,0),P4n+3(4n+3,-$\sqrt{3}$),P4n+4(4n+4,0).
∵2015=4×503+3,
∴P2015为(2015,-$\sqrt{3}$).
故选C.
点评 本题考查了规律型中的点的坐标,解题的关键是找出变化规律“P4n+1(4n+1,$\sqrt{3}$),P4n+2(4n+2,0),P4n+3(4n+3,-$\sqrt{3}$),P4n+4(4n+4,0)”.本题属于中档题,难度不大,解决该题型题目时,根据运动的规律找出点的坐标,根据坐标的变化找出坐标变化的规律是关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
8. 如图,直线AB与CD相交于点O.
如图,直线AB与CD相交于点O.
(1)若∠AOD+∠COB=2(∠BOD+∠AOC),求∠AOD,∠BOD的度数.
(2)若∠COB-∠BOD=m°,求∠AOD,∠BOD的度数(用含m°的式子表示)
 如图,直线AB与CD相交于点O.
如图,直线AB与CD相交于点O.(1)若∠AOD+∠COB=2(∠BOD+∠AOC),求∠AOD,∠BOD的度数.
(2)若∠COB-∠BOD=m°,求∠AOD,∠BOD的度数(用含m°的式子表示)
6.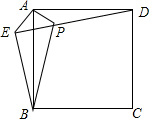 已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:
已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:
①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{2}$;
③EB⊥ED;
④S正方形ABCD=4+$\sqrt{6}$;
⑤S△APD+S△APB=1+$\sqrt{6}$,
其中正确结论的序号是( )
 已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:
已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{2}$;
③EB⊥ED;
④S正方形ABCD=4+$\sqrt{6}$;
⑤S△APD+S△APB=1+$\sqrt{6}$,
其中正确结论的序号是( )
| A. | ①③④ | B. | ①②⑤ | C. | ③④⑤ | D. | ①③⑤ |
10.五一期间,绿化部门预在县城主要干道旁边种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵,求A、B两种花木的数量分别是多少棵?若设A,B花木各x棵,y棵,则有( )
| A. | $\left\{\begin{array}{l}{x+y=6600}\\{x=2y+600}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=6600}\\{y=2x+600}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=6600}\\{y=2x-600}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=6600}\\{x=2y-600}\end{array}\right.$ |
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论: 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P,求证:
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P,求证: