题目内容
已知抛物线y=
x2+(k+
)x+k+1(k为常数)与x轴交于A(x1,0)、B(x2,0)(x1<0<x2),与y轴交于C,且满足(OA+OB)2=OC2+16,求此抛物线的解析式.
| 1 |
| 2 |
| 1 |
| 2 |
考点:抛物线与x轴的交点
专题:计算题
分析:根据题意表示出OA与OB,以及OC,代入已知等式中求出k的值,即可确定出抛物线解析式.
解答:解:∵抛物线y=
x2+(k+
)x+k+1(k为常数)与x轴交于A(x1,0)、B(x2,0)(x1<0<x2),与y轴交于C,
∴OA=-x1,OB=x2,OC=-k+1,且x1+x2=-
=-2k-1,x1x2=2k+2,
∵(OA+OB)2=OC2+16,
∴(-x1+x2)2=OC2+16,
∴(-x1+x2)2=(x1+x2)2-4x1x2=(2k+1)2-4(2k+2)=(-k+1)2+16,
解得:k1=-2,k2=4,
∵x1<0<x2,
∴x1•x2=2(k+1)<0,即k<-1,
∴k=-2,
∴抛物线解析式为y=
x2-
x-1.
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=-x1,OB=x2,OC=-k+1,且x1+x2=-
k+
| ||
|
∵(OA+OB)2=OC2+16,
∴(-x1+x2)2=OC2+16,
∴(-x1+x2)2=(x1+x2)2-4x1x2=(2k+1)2-4(2k+2)=(-k+1)2+16,
解得:k1=-2,k2=4,
∵x1<0<x2,
∴x1•x2=2(k+1)<0,即k<-1,
∴k=-2,
∴抛物线解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
点评:此题考查了抛物线与x轴的交点,熟练掌握韦达定理是解本题的关键.

练习册系列答案
相关题目
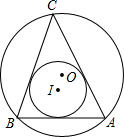 如图,在△ABC中,AB=5,AC=8,∠CAB=60°,求△ABC的内切圆⊙I的半径和外接圆⊙O的半径.
如图,在△ABC中,AB=5,AC=8,∠CAB=60°,求△ABC的内切圆⊙I的半径和外接圆⊙O的半径.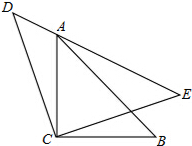 如图,△CAB和△CDE都是等腰直角三角形(C是直角顶点),点A在DE边上,求证:AD2+AE2=2AC2.
如图,△CAB和△CDE都是等腰直角三角形(C是直角顶点),点A在DE边上,求证:AD2+AE2=2AC2.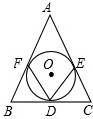 如图,⊙O与△ABC的三边都相切,切点分别为D、E、F,如果∠FDE=70°,那么∠A是多少度?
如图,⊙O与△ABC的三边都相切,切点分别为D、E、F,如果∠FDE=70°,那么∠A是多少度?
 已知:如图,在△ABC中,BC=2,∠A=45°,∠B=60°,求AC的长.
已知:如图,在△ABC中,BC=2,∠A=45°,∠B=60°,求AC的长.