题目内容
已知⊙O的半径为2,弦AB=2
.求弦AB及
所组成的弓形的面积.
| 3 |
 |
| AB |
考点:扇形面积的计算
专题:
分析:由OC⊥AB,得到AC=BC=
,再根据勾股定理计算出OC=1,这样可得到∠AOB=120°,而S弓形AB=S扇形OAB-S△AOB,然后利用扇形和三角形的面积公式计算即可.
| 3 |
解答: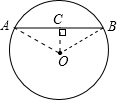 解:如图,
解:如图,
∵OC⊥AB,
∴AC=BC,
而弦AB=2
,
∴AC=
,
又∵⊙O的半径长为2,
∴OC=
=1,
∴∠A=30°,
∴∠AOB=120°,
∴S弓形AB=S扇形OAB-S△AOB=
-
×1×2
=(
π-
).
所以弓形AB的面积
π-
;
 解:如图,
解:如图,∵OC⊥AB,
∴AC=BC,
而弦AB=2
| 3 |
∴AC=
| 3 |
又∵⊙O的半径长为2,
∴OC=
22-(
|
∴∠A=30°,
∴∠AOB=120°,
∴S弓形AB=S扇形OAB-S△AOB=
| 120π×22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
所以弓形AB的面积
| 4 |
| 3 |
| 3 |
点评:本题考查了扇形的面积公式:S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S=
lR,l为扇形的弧长,R为半径.也考查了垂径定理和勾股定理以及圆的定义.
| nπR2 |
| 360 |
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知AB是⊙O的切线,在下列给出的条件中,能判断出AB⊥CD的是( )
| A、AB与⊙O相切于点C |
| B、CD是⊙O的直径 |
| C、AB与⊙O相切于点C,CD是直径 |
| D、CD是⊙O的弦 |
 将两张宽度都为1的纸条叠放成如图所示的图形,所成四边形的锐角为α,则这个四边形的面积为( )
将两张宽度都为1的纸条叠放成如图所示的图形,所成四边形的锐角为α,则这个四边形的面积为( )A、
| ||
| B、tanα | ||
C、
| ||
D、
|
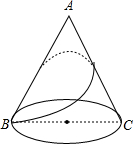 有一圆锥形粮堆如图所示,其母线长为12m,底面直径长为6m,一只小猫从B处绕粮堆巡视一圈后又回到B处,则它所行走最短路程是
有一圆锥形粮堆如图所示,其母线长为12m,底面直径长为6m,一只小猫从B处绕粮堆巡视一圈后又回到B处,则它所行走最短路程是