题目内容
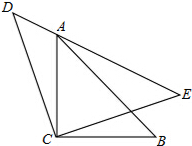 如图,△CAB和△CDE都是等腰直角三角形(C是直角顶点),点A在DE边上,求证:AD2+AE2=2AC2.
如图,△CAB和△CDE都是等腰直角三角形(C是直角顶点),点A在DE边上,求证:AD2+AE2=2AC2.考点:全等三角形的判定与性质,勾股定理
专题:证明题
分析:连结BE,根据等边三角形的性质就可以得出△ADC≌△BEC,就可以得出AD=BE,∠D=∠BEC,由等腰直角三角形的性质就可以得出∠AEB=90°,由勾股定理就可以得出结论.
解答: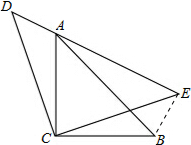 证明:连结BE,
证明:连结BE,
∵△ACB与△DCE都是等腰直角三角形,
∴∠DCE=∠ACB=90°,∠D=∠AEC=∠CAB=45°,
DC=EC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD-ACE=∠ACB-∠ACE,
∴∠ACD=∠BCE.
在△ADC和△BEC中,
,
∴△ADC≌△BEC(SAS).
∴AD=BE,∠D=∠BEC.
∴∠BEC=45°,
∴∠BEC+∠AEC=90°,
即∠AEB=90°.
∴AE2+BE2=AB2,
∴AE2+AD2=2AC2.
 证明:连结BE,
证明:连结BE,∵△ACB与△DCE都是等腰直角三角形,
∴∠DCE=∠ACB=90°,∠D=∠AEC=∠CAB=45°,
DC=EC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD-ACE=∠ACB-∠ACE,
∴∠ACD=∠BCE.
在△ADC和△BEC中,
|
∴△ADC≌△BEC(SAS).
∴AD=BE,∠D=∠BEC.
∴∠BEC=45°,
∴∠BEC+∠AEC=90°,
即∠AEB=90°.
∴AE2+BE2=AB2,
∴AE2+AD2=2AC2.
点评:本题考查了等腰直角三角形的性质的运用,直角三角形的判定及性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )
| A、4cm |
| B、2cm |
| C、4cm或2cm |
| D、小于或等于4cm,且大于或等于2cm |
已知AB是⊙O的切线,在下列给出的条件中,能判断出AB⊥CD的是( )
| A、AB与⊙O相切于点C |
| B、CD是⊙O的直径 |
| C、AB与⊙O相切于点C,CD是直径 |
| D、CD是⊙O的弦 |
 将两张宽度都为1的纸条叠放成如图所示的图形,所成四边形的锐角为α,则这个四边形的面积为( )
将两张宽度都为1的纸条叠放成如图所示的图形,所成四边形的锐角为α,则这个四边形的面积为( )A、
| ||
| B、tanα | ||
C、
| ||
D、
|
 如图,在正方形ABCD中,取AD,CD的边的中点E,F,连接CE,BF交于点G,连接AG,试判断AG与AB是否相等,并说明理由.
如图,在正方形ABCD中,取AD,CD的边的中点E,F,连接CE,BF交于点G,连接AG,试判断AG与AB是否相等,并说明理由. 在圆O中,∠ACB=∠BCA=60°,AC=2
在圆O中,∠ACB=∠BCA=60°,AC=2 如图,一块含有30°的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到△A′B′C′的位置,若BC=3cm,则:
如图,一块含有30°的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到△A′B′C′的位置,若BC=3cm,则: