题目内容
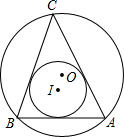 如图,在△ABC中,AB=5,AC=8,∠CAB=60°,求△ABC的内切圆⊙I的半径和外接圆⊙O的半径.
如图,在△ABC中,AB=5,AC=8,∠CAB=60°,求△ABC的内切圆⊙I的半径和外接圆⊙O的半径.考点:三角形的内切圆与内心,三角形的外接圆与外心
专题:
分析:连接AI,设AB圆的切点为E,连接IE,解直角三角形ATE即可内切圆的半径;连接CO交AB于D,连接AO,利用勾股定理即可求出AO的长.
解答: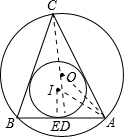 解:连接AI,设AB圆的切点为E,连接IE,
解:连接AI,设AB圆的切点为E,连接IE,
∵I是圆的内心,
∴∠EID=
∠CAB=30°,AE=BE=
AB=2.5,
∴IE=
AE=
×
=
,
∴△ABC的内切圆⊙I的半径是
;
连接CO交AB于D,连接AO,
∵AB=5,AC=8,
∴CD=
=
,
设AO=x,则OD=CD-OC=
-x,
在Rt△AOD中,OA2=OD2+AD2,
即x2=(
-x)2+2.52,
解得x=
.
∴外接圆⊙O的半径是
.
 解:连接AI,设AB圆的切点为E,连接IE,
解:连接AI,设AB圆的切点为E,连接IE,∵I是圆的内心,
∴∠EID=
| 1 |
| 2 |
| 1 |
| 2 |
∴IE=
| ||
| 3 |
| ||
| 3 |
| 5 |
| 2 |
5
| ||
| 6 |
∴△ABC的内切圆⊙I的半径是
5
| ||
| 6 |
连接CO交AB于D,连接AO,
∵AB=5,AC=8,
∴CD=
| AC2-AD2 |
| ||
| 2 |
设AO=x,则OD=CD-OC=
| ||
| 2 |
在Rt△AOD中,OA2=OD2+AD2,
即x2=(
| ||
| 2 |
解得x=
256
| ||
| 924 |
∴外接圆⊙O的半径是
256
| ||
| 924 |
点评:此题主要考查等腰三角形外接圆半径的求法以及内切圆半径求法,正确利用勾股定理以及等腰三角形的性质是解题关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )
| A、4cm |
| B、2cm |
| C、4cm或2cm |
| D、小于或等于4cm,且大于或等于2cm |
已知AB是⊙O的切线,在下列给出的条件中,能判断出AB⊥CD的是( )
| A、AB与⊙O相切于点C |
| B、CD是⊙O的直径 |
| C、AB与⊙O相切于点C,CD是直径 |
| D、CD是⊙O的弦 |
