题目内容
9.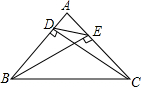 如图,△ABC中,DC⊥AB于D,BE⊥AC于E,试说明$\frac{DE}{BC}$=$\frac{AE}{AB}$.
如图,△ABC中,DC⊥AB于D,BE⊥AC于E,试说明$\frac{DE}{BC}$=$\frac{AE}{AB}$.
分析 先证明△AEB∽△ADC,再证明△ADE∽△ACB,即可解决问题.
解答 证明:∵DC⊥AB于D,BE⊥AC于E,
∴∠AEB=∠ADC=90°,
∵∠A=∠A,
∴△AEB∽△ADC,
∴$\frac{AE}{AD}$=$\frac{AB}{AC}$,
∴$\frac{AE}{AB}$=$\frac{AD}{AC}$,∵∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}$=$\frac{AE}{AB}$.
点评 本题考查相似三角形的判定和性质,解题的关键是灵活运用相似三角形的判定和性质解决问题,属于中考常考题型.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
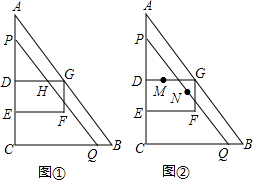
 如图,在正方形ABCD中,取AD、CD边的中点E,F,连接CE,BF交于点G,连接AG.证明:AG=AB.
如图,在正方形ABCD中,取AD、CD边的中点E,F,连接CE,BF交于点G,连接AG.证明:AG=AB.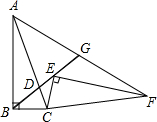 如图,在Rt△ABC中,∠ABC=90°,sin∠BAC=$\frac{1}{3}$,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G.
如图,在Rt△ABC中,∠ABC=90°,sin∠BAC=$\frac{1}{3}$,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G.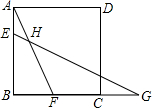 如图,在边长为6的正方形ABCD中,E、F、G分别是AB、BC、和BC延长线上的点,若AE=BF=CG=2,连接EG、AF交于点H,则AH的长为$\frac{4\sqrt{10}}{5}$.
如图,在边长为6的正方形ABCD中,E、F、G分别是AB、BC、和BC延长线上的点,若AE=BF=CG=2,连接EG、AF交于点H,则AH的长为$\frac{4\sqrt{10}}{5}$.



 如图,一次函数y=kx-3的图象经过点M.
如图,一次函数y=kx-3的图象经过点M.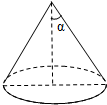 如图,圆锥的母线长为11cm,侧面积为55πcm2,设圆锥的母线与高的夹角为α,则cosα的值为$\frac{4\sqrt{6}}{11}$.
如图,圆锥的母线长为11cm,侧面积为55πcm2,设圆锥的母线与高的夹角为α,则cosα的值为$\frac{4\sqrt{6}}{11}$.