题目内容
4.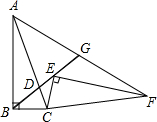 如图,在Rt△ABC中,∠ABC=90°,sin∠BAC=$\frac{1}{3}$,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G.
如图,在Rt△ABC中,∠ABC=90°,sin∠BAC=$\frac{1}{3}$,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G.(1)求证:△BCD∽△AGD;
(2)求AG的长.
分析 (1)作BH⊥CD于H,如图,然后根据旋转的性质的∠BCE=∠ACF,CB=CE,CA=CF,根据两等腰三角形的两顶角相等,则底角相等得到∠CBE=∠CAF,∠AGD=∠BCD,于是得到结论;
(2)在Rt△ABC中利用∠BAC的正弦可计算出AC=6,由于BC=BD=2,根据等腰三角形的性质得CH=DH,根据等角的余角相等得∠HBC=∠BAC,在Rt△HBC中利用sin∠HBC的正弦可计算出HC=$\frac{1}{3}$BC=$\frac{2}{3}$,则CD=2CH=$\frac{4}{3}$,所以AD=AC-CD=$\frac{14}{3}$,易得∠AGD=∠BCD,再利用∠BCD=∠BDC可得∠ADG=∠AGD,于是根据等腰三角形的性质可得AG=AD=$\frac{14}{3}$.
解答 解:(1) 作BH⊥CD于H,如图,
作BH⊥CD于H,如图,
∵Rt△ABC绕点C旋转到Rt△FEC的位置,
∴∠BCE=∠ACF,CB=CE,CA=CF,
∴∠CBE=$\frac{1}{2}$(180°-∠BCE),∠CAF=$\frac{1}{2}$(180°-∠ACF),
∴∠CBE=∠CAF,
∵∠BDC=∠ADG,
∴△BCD∽△AGD;
(2)在Rt△ABC中,∠ABC=90°,∵sin∠BAC=$\frac{BC}{AC}=\frac{1}{3}$,
∴AC=3BC=6,
∵BC=BD=2,
∴CH=DH,
∵∠HBC+∠ACB=90°,∠BAC+∠ACB=90°,
∴∠HBC=∠BAC,
∴sin∠HBC=$\frac{1}{3}$,
在Rt△HBC中,∵sin∠HBC=$\frac{HC}{BC}=\frac{1}{3}$,
∴HC=$\frac{1}{3}$BC=$\frac{2}{3}$,
∴CD=2CH=$\frac{4}{3}$,
∴AD=AC-CD=6-$\frac{4}{3}$=$\frac{14}{3}$,
∵∠BDC=∠ADG,
∴∠AGD=∠BCD,
∵BC=BD,
∴∠BCD=∠BDC,
∴∠ADG=∠AGD,
∴AG=AD=$\frac{14}{3}$.
点评 本题考查了相似三角形的判定和性质,旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和解直角三角形.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案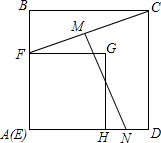 如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )
如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )| A. | $\frac{25}{4}$cm | B. | $\frac{73}{4}$cm | C. | $\frac{\sqrt{73}}{2}$cm | D. | $\frac{\sqrt{75}}{2}$cm |
| A. | a3+a3=26a | B. | 3a-2a=a | C. | 3a2b-4b2a=-a2b | D. | (-a)2=-a2 |
 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )| A. | 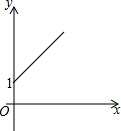 | B. | 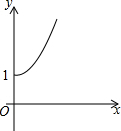 | C. | 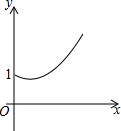 | D. | 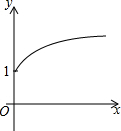 |
| A. | 0.129×105 | B. | 11.29×103 | C. | 1.129×104 | D. | 1.129×105 |
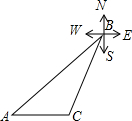 如图,某海洋区域内有A、B两个小岛,其中A岛在B岛的西南方向,一天,一只轮船上午8时从A岛出发,沿正东方向以每小时80海里的速度航行1.5小时到达C处,此时轮船在B岛的南偏西15°方向,试求A、B两岛相距多少海里?(结果保留根号)(注:E-东方,W-西方,S-南方,N-北方)
如图,某海洋区域内有A、B两个小岛,其中A岛在B岛的西南方向,一天,一只轮船上午8时从A岛出发,沿正东方向以每小时80海里的速度航行1.5小时到达C处,此时轮船在B岛的南偏西15°方向,试求A、B两岛相距多少海里?(结果保留根号)(注:E-东方,W-西方,S-南方,N-北方)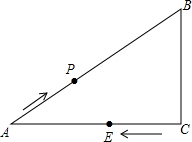 如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢?
如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢?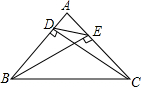 如图,△ABC中,DC⊥AB于D,BE⊥AC于E,试说明$\frac{DE}{BC}$=$\frac{AE}{AB}$.
如图,△ABC中,DC⊥AB于D,BE⊥AC于E,试说明$\frac{DE}{BC}$=$\frac{AE}{AB}$.