题目内容
12. 如图,在正方形ABCD中,取AD、CD边的中点E,F,连接CE,BF交于点G,连接AG.证明:AG=AB.
如图,在正方形ABCD中,取AD、CD边的中点E,F,连接CE,BF交于点G,连接AG.证明:AG=AB.
分析 如图,连接EB,先证明△DEC≌△CFB,△AEB≌CFB,得∠DEC=∠CFB,∠AEB=∠BFC,由∠DEC+∠DCE=90°,∠CFB+∠DCE=90°推出∠FGC=∠EGB=90°,再证明A、B、G、E四点共圆,得∠AGB=∠AEB,由此可以证明∠AGB=∠ABG.
解答 证明:如图,连接EB. ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=AD=CD,∠D=∠DAB=∠ABC=∠BCF=90°,
∵AE=DE,DF=FC,
∴AE=DE=DF=FC
在△DEC和△CFB中,
$\left\{\begin{array}{l}{DE=CF}\\{∠D=∠BCF}\\{DC=BC}\end{array}\right.$,
∴△DEC≌△CFB,
同理△AEB≌CFB,
∴∠DEC=∠CFB,∠AEB=∠BFC
∵∠DEC+∠DCE=90°,
∴∠CFB+∠DCE=90°
∴∠FGC=∠EGB=90°,
∴∠EAB+∠EGB=180°,
∴A、B、G、E四点共圆,
∴∠AGB=∠AEB=∠BFC,
∵CD∥AB,
∴∠BFC=∠FBA,
∴∠AGB=∠ABG,
∴AG=AB.
点评 本题考查正方形的性质、全等三角形的判定和性质、四点共圆等知识,解题的关键是四点共圆的发现,为证明角相等提供了方便,属于中考常考题型.

练习册系列答案
相关题目
7.一个扇形占其所在圆的面积的$\frac{1}{8}$,则该扇形圆心角是( )
| A. | 225° | B. | 45° | C. | 60° | D. | 无法计算 |
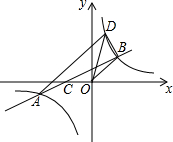 如图,点A和点B分别是反比例函数y=$\frac{k}{x}$(k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=$\frac{1}{2}$,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=$\frac{k}{x}$于点D,连接OD,BD.
如图,点A和点B分别是反比例函数y=$\frac{k}{x}$(k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=$\frac{1}{2}$,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=$\frac{k}{x}$于点D,连接OD,BD.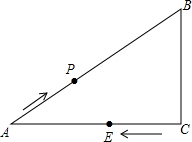 如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢?
如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢? 如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象上的点,连接0A作0A⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.
如图,已知点A(1,2)是函数y=$\frac{2}{x}$(x>0)的图象上的点,连接0A作0A⊥0B,与图象y=$\frac{-6}{x}$(x>0)交于点B.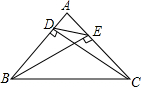 如图,△ABC中,DC⊥AB于D,BE⊥AC于E,试说明$\frac{DE}{BC}$=$\frac{AE}{AB}$.
如图,△ABC中,DC⊥AB于D,BE⊥AC于E,试说明$\frac{DE}{BC}$=$\frac{AE}{AB}$.