题目内容
17.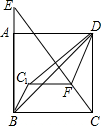 如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.
如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.
分析 如图建立如图坐标系,连接CC1,DF的延长线交CC1于M,作FH⊥BC于H.想办法求出点C1的坐标,根据S△BDC=${S}_{△BC{C}_{1}}$+${S}_{△CD{C}_{1}}$-S△BCD计算即可.
解答 解:如图建立如图坐标系,连接CC1,DF的延长线交CC1于M,作FH⊥BC于H.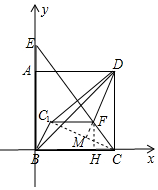
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=5,
∵AE=$\frac{AB}{3}$=$\frac{5}{3}$,
∴BE=$\frac{20}{3}$,
在Rt△BCE中,EC=$\sqrt{B{E}^{2}+B{C}^{2}}$=$\frac{25}{3}$,
∵FH∥BE,
∴$\frac{CF}{CE}$=$\frac{FH}{BE}$=$\frac{CH}{BC}$,
∴$\frac{\frac{5}{2}}{\frac{25}{3}}$=$\frac{FH}{\frac{20}{3}}$=$\frac{CH}{5}$,
∴FH=2,CH=$\frac{3}{2}$,
∴BH=BC-CH=$\frac{7}{2}$,
∴F($\frac{7}{2}$,2),∵D(5,5),
∴直线DF的解析式为y=2x-5,
∵CC1⊥DF,
∴直线CC1的解析式为y=-$\frac{1}{2}$x+$\frac{5}{2}$,
由$\left\{\begin{array}{l}{y=2x-5}\\{y=-\frac{1}{2}x+\frac{5}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
∴点M的坐标为(3,1),
∵MC=MC1,
∴C1(1,2),
∴S△BDC=${S}_{△BC{C}_{1}}$+${S}_{△CD{C}_{1}}$-S△BCD=$\frac{1}{2}$×5×2+$\frac{1}{2}$×5×4-$\frac{1}{2}$×5×5=$\frac{5}{2}$,
故答案为$\frac{5}{2}$.
点评 本题考查正方形的性质、翻折变换、坐标与图形、一次函数的应用、中点坐标公式等知识,解题的关键是学会构建平面直角坐标系,利用一次函数解决问题,属于中考填空题中的压轴题.

| A. | 平移 | B. | 旋转 | C. | 轴对称 | D. | 相似 |
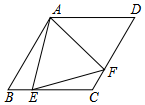 如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于$\frac{19\sqrt{3}}{4}$.
如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于$\frac{19\sqrt{3}}{4}$.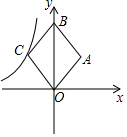 如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( ) 足球比赛中,守门员根据场上攻守情况在门前来回跑动,若以球门线为基准,向前跑记作正数,返回跑记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上)
足球比赛中,守门员根据场上攻守情况在门前来回跑动,若以球门线为基准,向前跑记作正数,返回跑记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上)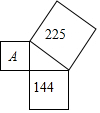 如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为81.
如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为81.