题目内容
5.某市对城区沿江两岸的共1200米路段进行亮化工程建设,整个工程拟由甲、乙两个安装公司共同完成.若两个公司合做,则恰好用12天完成;若甲、乙合做9天后,由甲再单独做5天也恰好完成.已知需要支付甲、乙两公司的工程费用分别为200元/米和175元/米.(1)甲、乙两公司单独完成这项工程各需多少天?
(2)要使整个工程费用不超过22.5万元,则乙公司最少应施工多少天?
分析 (1)通过理解题意可知本题存在两个等量关系,即“若两个公司合做,则恰好用12天完成”和“若甲、乙合做9天后,由甲再单独做5天也恰好完成”,根据这两个等量关系可列出方程组.
(2)在(1)的基础上,可知“甲乙合作必须完成”和“总费用不超过22.5万元”据此列方程和不等式,进行解答.
解答 解:(1)设甲公司单独做需x天完成,乙公司单独做需y天完成
则$\frac{1}{x}$+$\frac{1}{y}$=$\frac{1}{12}$,将方程两边同乘以14得$\frac{14}{x}$+$\frac{14}{y}$=$\frac{14}{12}$=$\frac{7}{6}$①,
$\frac{9}{x}$+$\frac{9}{y}$+$\frac{5}{x}$=1.
合并同类项得$\frac{14}{x}$+$\frac{9}{y}$=1 ②,
用①-②得$\frac{5}{y}$=$\frac{1}{6}$,
解得y=30,
再将y=30代入①式或②式都可求出x=20.
经检验:x=20,y=30是分式方程的解,
答:甲公司单独做需20天完成,乙公司单独做需30天完成.
(2)设甲安装公司安装m天,乙公司安装n天可以完成这项工程.
$\frac{m}{20}$+$\frac{n}{30}$=1①,
1.2m+0.7n≤22.5②,
由①得3m+2n=60,
∴m=$\frac{60-2n}{3}$③.
把③代入②,得1.2×$\frac{60-2n}{3}$+0.7n≤22.5,
∴24-0.8n+0.7n≤22.5,
∴0.1n≥1.5,
∴n≥15.
答:乙公司最少施工15天.
点评 此题主要考查了分式方程和不等式的应用,关键是正确理解题意,找出题目中的等量关系和不等关系,再列出方程和不等式.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案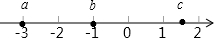 已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )| A. | a=-3 | B. | b=-1 | C. | a的相反数为正数 | D. | c可能等于2.5 |
 请作出一次函数y=x+1的图象.
请作出一次函数y=x+1的图象.| x | … | … | |||||
| y | … | … |
 如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.
如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米. 如图,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-3.
如图,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-3. 如图,已知AB=CD,AD=BC,现有下列结论:
如图,已知AB=CD,AD=BC,现有下列结论: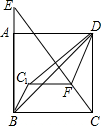 如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.
如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$. 用长32米的篱笆围成面积为130m2的矩形场地,矩形场地的一面利用墙可用最大长度为16m,与墙平行的对边有1m长的一道门,求此矩形场地的长、宽各是多少米?
用长32米的篱笆围成面积为130m2的矩形场地,矩形场地的一面利用墙可用最大长度为16m,与墙平行的对边有1m长的一道门,求此矩形场地的长、宽各是多少米?