题目内容
7.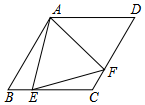 如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于$\frac{19\sqrt{3}}{4}$.
如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于$\frac{19\sqrt{3}}{4}$.
分析 连接AC,由菱形ABCD中,∠D=60°,根据菱形的性质,易得△ADC是等边三角形,证明△ADF≌△ACE,可得到:SAECF=S△ADC,EC=DF和菱形的边长,求出S△ACD、S△ECF,根据面积间关系即可求出△AEF的面积.
解答 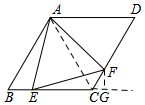 证明:如图,连接AC,
证明:如图,连接AC,
∵在菱形ABCD中,∠D=60°,AD=DC,
∴△ADC是等边三角形,
∵AC是菱形的对角线,
∴∠ACB=$\frac{1}{2}$∠DCB=60°,
∵∠FAC+∠EAC=∠FAC+∠DAF=60°,
∴∠EAC=∠DAF,
在△ADF和△ACE中,
∵$\left\{\begin{array}{l}{∠D=∠ACB}\\{AD=AC}\\{∠DAF=∠CAE}\end{array}\right.$,
∴△ADF≌△ACE(ASA),
∴DF=CE=3,AE=AF,BC=BE+CE=AB=5.
∴S四边形AECF=S△ACD
=$\frac{1}{2}$×5×5×sin60°
=$\frac{25}{4}\sqrt{3}$,
如图,过F作FG⊥BC于G,则
S△ECF=$\frac{1}{2}$CE•CF•sin∠GCF
=$\frac{1}{2}$CE•CF•sin60°
=$\frac{1}{2}$•6•$\frac{\sqrt{3}}{2}$
=$\frac{3}{2}\sqrt{3}$,
∴S△AEF=S四边形AECF-S△ECF
=$\frac{25}{4}\sqrt{3}$-$\frac{3}{2}\sqrt{3}$
=$\frac{19}{4}\sqrt{3}$.
故答案为:$\frac{19}{4}\sqrt{3}$.
点评 本题考查了菱形的性质、等边三角形的判定与性质、全等三角形的判定与性质以及及三角形的面积的计算.准确作出辅助线构造全等三角形,利用图形间的面积关系是解决本题的关键.

| A. | 130° | B. | 80° | C. | 140°或40° | D. | 60°或120° |
| A. |  | B. |  | C. |  | D. |  |
 如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.
如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.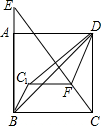 如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.
如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.