题目内容
9. 足球比赛中,守门员根据场上攻守情况在门前来回跑动,若以球门线为基准,向前跑记作正数,返回跑记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上)
足球比赛中,守门员根据场上攻守情况在门前来回跑动,若以球门线为基准,向前跑记作正数,返回跑记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上)(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)这段时间内,这位守门员一共跑动多少米?
分析 (1)根据有理数的加法,可得答案;
(2)根据有理数的加法,可得每次与球门线的距离,根据有理数的大小比较,可得答案;
(3)求出所有数的绝对值的和即可.
解答 解:(1)+10-2+5-6+12-9+4-14=0,
答:守门员最后正好回到球门线上;
(2)第一次10,第二次10-2=8,第三次8+5=13,第四次13-6=7,第五次7+12=19,第六次19-9=10,第七次10+4=14,第八次14-14=0,
19>14>13>10>8>7,
答:守门员离开球门线的最远距离达19米;
(3)10+2+5+6+12+9+4+14=62米.
答:这位守门员一共跑动62米.
点评 本题考查了正数和负数,(1)利用了有理数的加减法运算,(2)利用了有理数的加减法运算,有理数的大小比较,(3)利用了有理数的加法运算.

练习册系列答案
相关题目
20.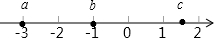 已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
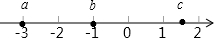 已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )| A. | a=-3 | B. | b=-1 | C. | a的相反数为正数 | D. | c可能等于2.5 |
4.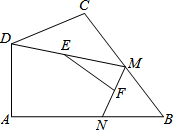 如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
 如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )| A. | 2 | B. | 3 | C. | 4 | D. | $\sqrt{7}$ |
14. 请作出一次函数y=x+1的图象.
请作出一次函数y=x+1的图象.
 请作出一次函数y=x+1的图象.
请作出一次函数y=x+1的图象.| x | … | … | |||||
| y | … | … |
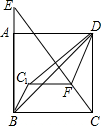 如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.
如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$. 如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长. 如图,将字母“V”向右平移2格会得到字母“W”.
如图,将字母“V”向右平移2格会得到字母“W”.