题目内容
 如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F,点G,H分别为AD,BC的中点,试证明EF和GH互相平分.
如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F,点G,H分别为AD,BC的中点,试证明EF和GH互相平分.考点:平行四边形的判定与性质
专题:证明题
分析:根据直角三角形斜边上的中线等于斜边的一半,以及等腰三角形的性质,即可证得∠GEF=∠BFH,则EG和FH平行且相等,即可证明四边形EHFG是平行四边形,从而证明EF和GH互相平分.
解答: 证明:∵AE⊥BD,G是AD的中点,即EG是直角△AED斜边AD上的中线,
证明:∵AE⊥BD,G是AD的中点,即EG是直角△AED斜边AD上的中线,
∴EG=
AD=DG,
同理,FH=
BC=BH,
又∵平行四边形ABCD中,AD=BC,
∴EG=FH=DG=BH.
∴∠GDE=∠GED,∠FBH=∠BFH,
又∵平行四边形ABCD中,AD∥BC,
∴∠GDE=∠FBH,
∴∠GEF=∠BFH,
∴EG∥FH,
又∵EG=FH,
∴四边形EHFG是平行四边形,
∴EF和GH互相平分.
 证明:∵AE⊥BD,G是AD的中点,即EG是直角△AED斜边AD上的中线,
证明:∵AE⊥BD,G是AD的中点,即EG是直角△AED斜边AD上的中线,∴EG=
| 1 |
| 2 |
同理,FH=
| 1 |
| 2 |
又∵平行四边形ABCD中,AD=BC,
∴EG=FH=DG=BH.
∴∠GDE=∠GED,∠FBH=∠BFH,
又∵平行四边形ABCD中,AD∥BC,
∴∠GDE=∠FBH,
∴∠GEF=∠BFH,
∴EG∥FH,
又∵EG=FH,
∴四边形EHFG是平行四边形,
∴EF和GH互相平分.
点评:本题考查了直角三角形的性质,以及平行四边形的判定与性质,证明两线段互相平分的问题常用的思路是转化为证明平行四边形的问题.

练习册系列答案
相关题目
 图中,同旁内角的对数为( )
图中,同旁内角的对数为( )| A、14 | B、16 | C、18 | D、20 |
 如图:AB⊥CD,CD为⊙O直径,且AB=20,CE=4,那么⊙O的半径是( )
如图:AB⊥CD,CD为⊙O直径,且AB=20,CE=4,那么⊙O的半径是( )A、
| ||
| B、14 | ||
C、
| ||
| D、15 |
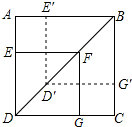 如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′.
如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′. 如图,A,B是小河同侧的两个村庄,为解决吃水问题,两村合资在河边修一个水站.
如图,A,B是小河同侧的两个村庄,为解决吃水问题,两村合资在河边修一个水站.