题目内容
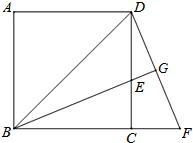 如图,四边形ABCD是正方形,点F在BC延长线上,且BF=BD,G为DF中点,BG与DC交于点E,以下结论正确的有
如图,四边形ABCD是正方形,点F在BC延长线上,且BF=BD,G为DF中点,BG与DC交于点E,以下结论正确的有①△BCE≌△DCF ②E是CD中点
③△BCE∽△DGE ④2DG2=DE•DC.
考点:相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质
专题:
分析:证明BG⊥DF,结合∠BCD=90°得到B、C、G、D四点共圆,得到∠FDC=∠EBC;容易证明①③成立;②不成立;证明△DGE∽△DCF,列出比例式即可证明④成立.
解答: 解:∵BF=BD,G为DF中点,
解:∵BF=BD,G为DF中点,
∴BG⊥DF;
∵四边形ABCD为正方形,
∴∠BCD=90°,BC=CD;
∴B、C、G、D四点共圆,
∴∠FDC=∠EBC;而∠BEC=∠DEG,
∴△BCE∽△DGE,故③正确.
在△BCE与△DCF中,
,
∴△BCE≌△DCF(ASA),故①正确.
∵BF=BD,且BG⊥DF,
∴BG平分∠DBC,故②不正确.
∵∠GDE=∠CDF,∠DGE=∠DCF,
∴△DGE∽△DCF,
∴DG:DC=DE:DF,而DF=2DG,
∴2DG2=DE•DC.故④正确,
∴结论正确的有①③④.
故答案为①③④.
 解:∵BF=BD,G为DF中点,
解:∵BF=BD,G为DF中点,∴BG⊥DF;
∵四边形ABCD为正方形,
∴∠BCD=90°,BC=CD;
∴B、C、G、D四点共圆,
∴∠FDC=∠EBC;而∠BEC=∠DEG,
∴△BCE∽△DGE,故③正确.
在△BCE与△DCF中,
|
∴△BCE≌△DCF(ASA),故①正确.
∵BF=BD,且BG⊥DF,
∴BG平分∠DBC,故②不正确.
∵∠GDE=∠CDF,∠DGE=∠DCF,
∴△DGE∽△DCF,
∴DG:DC=DE:DF,而DF=2DG,
∴2DG2=DE•DC.故④正确,
∴结论正确的有①③④.
故答案为①③④.
点评:该题以正方形为载体,主要考查了相似三角形的判定及其性质等几何知识点的应用问题;牢固掌握有关定理是灵活解决问题的基础和关键.

练习册系列答案
相关题目
下列正确的是( )
| A、-2ab2的系数是-2 |
| B、32ab3的次数是6次 |
| C、37ab5是多项式 |
| D、x2+x-1的常数项为1 |
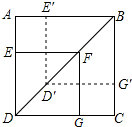 如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′.
如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′. 如图,A,B是小河同侧的两个村庄,为解决吃水问题,两村合资在河边修一个水站.
如图,A,B是小河同侧的两个村庄,为解决吃水问题,两村合资在河边修一个水站.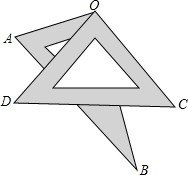 如图,将一副三角板叠放在一起,使直角顶点重合于O点,则∠AOC+∠BOD=
如图,将一副三角板叠放在一起,使直角顶点重合于O点,则∠AOC+∠BOD=