题目内容
 如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.(1)如果P,Q分别从A,B两点同时出发,经过x秒钟,△PBQ的面积等于8厘米2,求此时x的值;
(2)如果P,Q两点分别从A,B两点同时出发,并且P到B后又继续在BC边上前进,Q到C后又继续在CA边上前进,经过8秒钟,△PCQ的面积等于多少厘米2?
考点:一元二次方程的应用
专题:几何动点问题
分析:(1)根据△PBQ的面积等于8厘米2列出方程,解方程即可;
(2)结合题意先画出图形,根据勾股定理求出AC的长,再过点Q作QD⊥BC,交BC于点D,所以QD∥AB,得出
=
从而求得QD的长,运用三角形的面积公式即可求△PCQ的面积.
(2)结合题意先画出图形,根据勾股定理求出AC的长,再过点Q作QD⊥BC,交BC于点D,所以QD∥AB,得出
| QD |
| AB |
| CQ |
| AC |
解答:解:(1)∵△PBQ的面积等于8厘米2,
∴
(6-x)•2x=8,
解得x1=2,x2=4(不合题意舍去),
答:经过2秒钟,△PBQ的面积等于8厘米2;
(2)如图,

∵AB=6cm,BC=8cm,
∴AC=
=10cm.
根据题意知,经过8秒钟后,BP=2cm,CQ=8cm,
∴PC=6cm.
过点Q作QD⊥BC,交BC于点D,所以QD∥AB,
∴
=
,
即
=
,
解得QD=4.8,
S△PCQ=
×6×4.8=14.4.
∴△PCQ的面积为14.4厘米2.
∴
| 1 |
| 2 |
解得x1=2,x2=4(不合题意舍去),
答:经过2秒钟,△PBQ的面积等于8厘米2;
(2)如图,

∵AB=6cm,BC=8cm,
∴AC=
| AB2+BC2 |
根据题意知,经过8秒钟后,BP=2cm,CQ=8cm,
∴PC=6cm.
过点Q作QD⊥BC,交BC于点D,所以QD∥AB,
∴
| QD |
| AB |
| CQ |
| AC |
即
| QD |
| 6 |
| 8 |
| 10 |
解得QD=4.8,
S△PCQ=
| 1 |
| 2 |
∴△PCQ的面积为14.4厘米2.
点评:本题考查了一元二次方程的应用、三角形面积的求法以及动点问题.解题的关键是结合图形求解.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 把六张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为acm,宽为bcm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
把六张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为acm,宽为bcm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )| A、4bcm |
| B、(3a+b)cm |
| C、(2a+2b)cm |
| D、(a+3b)cm |
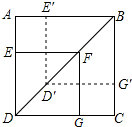 如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′.
如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′.