题目内容
13.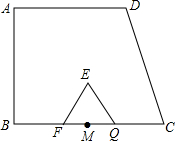 在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=4$\sqrt{3}$.点M是BC的中点.点P从点M出发沿MB以每秒1个单位的速度向点B匀速运动,到达点B后立刻以原速度沿BC运动到点C;点Q从点M出发以每秒1个单位的速度在射线NC上匀速运动.在点P,Q的运动过程中,以PQ为边作一个等边三角形EPQ,使△EPQ与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P到达点C时停止运动,点Q也随之停止.设点P,Q是运动时间为t秒(t>0).
在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=4$\sqrt{3}$.点M是BC的中点.点P从点M出发沿MB以每秒1个单位的速度向点B匀速运动,到达点B后立刻以原速度沿BC运动到点C;点Q从点M出发以每秒1个单位的速度在射线NC上匀速运动.在点P,Q的运动过程中,以PQ为边作一个等边三角形EPQ,使△EPQ与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P到达点C时停止运动,点Q也随之停止.设点P,Q是运动时间为t秒(t>0).(1)当BP=2时,写出PQ的长.
(2)当△EPQ的顶点E在AD边上时,求出t的取值范围.
(3)是否存在t的值,使得△EPQ的边经过CD的中点O?若存在,请直接写出t的值;若不存在,请说明理由.
分析 (1)分类讨论:当点P从M点向B点运动时,BM=$\frac{1}{2}$BC=4,由BP=2得PM=2,利用速度公式得1•t=2,解得t=2,则MQ=2,所以此时PQ=PM+QM=4;当点P从B点向M点运动时,由BP=2得PM=2,则1•t=2+4,解得t=6,所以MQ=6,于是得到PQ=PM+QM=8;
(2)过M点作MN⊥AD于N,如图1,则MN=AB=4$\sqrt{3}$,由于MB=MC=4,可计算出NB=NC=8,于是可判断△NBC为等边三角形,若点P运动到B点,Q点运动到C点时,点E在N点处,此时t=4,
当点P从B点向C点运动时,如图2,作EH⊥BC于H,则BP=t-4,MQ=4,PM=8-t,则可计算出PQ=8,由于△EPQ为等边三角形,则可计算出EH=$\frac{\sqrt{3}}{2}$PQ=4$\sqrt{3}$,于是判断点E在直线AD上,由于DN=AD-AN=2,于是可判断当4≤t≤6时,点E在线段ND上;
(3)分类讨论:当边EQ经过经过CD的中点O时,如图3,通过证明△ODE≌△OCQ得到DE=CQ,由于P点在B点时,E点在N点,则EN=BP=t-4,DE=6-t,CQ=6-t,所以4+6-t=t,解得t=5;当边EP经过经过CD的中点O时,如图4,同理可得PC=DE,易得DE=NE-ND=t-6,PC=12-t,则t-6=12-t,解得t=9.
解答 解:(1)当点P从M点向B点运动时,BM=$\frac{1}{2}$BC=4,
∵BP=2,
∴PM=4-2=2,即1•t=2,解得t=2,
∴MQ=2×1=2,
∴PQ=PM+QM=2+2=4;
当点P从B点向M点运动时,BM=4,
∵BP=2,PM=2,
∴1•t=2+4,解得t=6,
∴MQ=6×1=6,
∴PQ=PM+QM=2+6=8;
即PQ的长为4或8;
(2)过M点作MN⊥AD于N,如图1,则MN=AB=4$\sqrt{3}$,
∵MB=MC=4,
∴NB=NC=8,
∴△NBC为等边三角形,
∴点P运动到B点,Q点运动到C点时,点E在N点处,此时t=4,
当点P从B点向C点运动时,如图2,作EH⊥BC于H,则BP=t-4,MQ=4,
∴PM=4-(t-4)=8-t,
∴PQ=8-t+t=8,
∵△EPQ为等边三角形,
∴EH=$\frac{\sqrt{3}}{2}$PQ=4$\sqrt{3}$,
∴点E在直线AD上,
∵AN=BM=4,
∴DN=AD-AN=6-4=2,
∴当4≤t≤6时,点E在线段ND上,
即△EPQ的顶点E在AD边上;
(3)存在.
当边EQ经过经过CD的中点O时,如图3,
∵DE∥CQ,
∴∠D=∠QCO,
在△ODE和△OCQ中,
$\left\{\begin{array}{l}{∠D=∠QCO}\\{OD=OC}\\{∠DOE=∠COQ}\end{array}\right.$,
∴△ODE≌△OCQ,
∴DE=CQ,
∵BP=t-4,
而P点在B点时,E点在N点,
∴EN=BP=t-4,
∴DE=2-(t-4)=6-t,
∴CQ=6-t,
而MC=4,MQ=t,
∴4+6-t=t,解得t=5;
当边EP经过经过CD的中点O时,如图4,
同理可得PC=DE,
∵DE=NE-ND=t-4-2=t-6,
而PC=8-(t-6)=12-t,
∴t-6=12-t,解得t=9,
综上所述,当t=5s或9s时,△EPQ的边经过CD的中点.
点评 本题考查了四边形综合题:熟练掌握梯形和矩形的性质和等边三角形的性质;会利用代数式法解决有关动点问题;会运用分类讨论的思想解决数学问题.

| A. | 6,(-3,4) | B. | 2,(3,2) | C. | 2,(3,0) | D. | 1,(4,2) |
| A. | (m+1)2 | B. | m2+1 | C. | m2 | D. | m2-1 |
| A. | a-2•a-1=a2 | B. | (a2)-3=a-6 | ||
| C. | a2÷a-3=a5 | D. | a-n=($\frac{1}{a}$)n(n为正整数) |