题目内容
16.先化简,再求值:$\frac{{x}^{2}+1}{x+1}-\frac{2}{x+1}$,其中x=$\frac{1}{5}$.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{{x}^{2}+1-2}{x+1}$
=$\frac{{x}^{2}-1}{x+1}$
=$\frac{(x+1)(x-1)}{x+1}$
=x-1,
当x=$\frac{1}{5}$时,原式=$\frac{1}{5}$-1=-$\frac{4}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
7.方程x2-$\frac{1}{2}$x+$\frac{3}{2}$=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
4.不等式-3x≥6的解集在数轴上表示为( )
| A. |  | B. |  | C. | 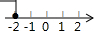 | D. | 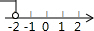 |
8.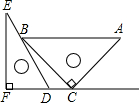 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )| A. | 25° | B. | 20° | C. | 15° | D. | 18° |
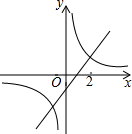 如图,反比例函数y1=$\frac{{k}_{1}}{x}$的图象与直线y2=k2x+b的一个交点的横坐标为2,当x=3时,y1<y2(填“>”、“=”或“<”).
如图,反比例函数y1=$\frac{{k}_{1}}{x}$的图象与直线y2=k2x+b的一个交点的横坐标为2,当x=3时,y1<y2(填“>”、“=”或“<”).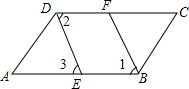 已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.说明AB∥DC的理由.
已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.说明AB∥DC的理由.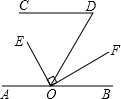 已知:OE平分∠AOD,AB∥CD,OF⊥OE于O,∠D=50°,则∠BOF=25°.
已知:OE平分∠AOD,AB∥CD,OF⊥OE于O,∠D=50°,则∠BOF=25°.