题目内容
6.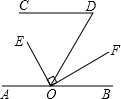 已知:OE平分∠AOD,AB∥CD,OF⊥OE于O,∠D=50°,则∠BOF=25°.
已知:OE平分∠AOD,AB∥CD,OF⊥OE于O,∠D=50°,则∠BOF=25°.
分析 利用平行线的性质首先得出∠D=∠DOB=50°,即可得出∠AOD的度数,再利用角平分线的性质得出∠AOE的度数,最后利用邻补角关系求出∠BOF的度数.
解答 解:∵AB∥CD,
∴∠D=∠DOB=50°,
∴∠AOD=180°-∠DOB=130°,
∵OE平分∠AOD,
∴∠AOE=$\frac{1}{2}$AOD=65°,
∵OF⊥OE于点O,
∴∠EOF=90°,
∴∠BOF=180°-∠EOF-∠AOE=25°.
故答案为:25°.
点评 此题主要考查了角平分线的性质以及平行线的性质等知识,根据已知得出∠AOE的度数是解题关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
17.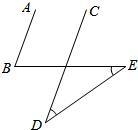 如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
 如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
14.一组数据3、3、5、2、7的中位数和平均数分别是( )
| A. | 3和3 | B. | 3和4 | C. | 4和3 | D. | 4和4 |
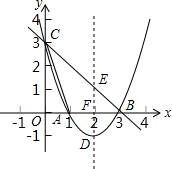 在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=-x沿y轴向上平移3个单位长度后恰好经过B,C两点.
在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=-x沿y轴向上平移3个单位长度后恰好经过B,C两点.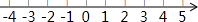 解不等式,并把解集表示在数轴上.
解不等式,并把解集表示在数轴上.