题目内容
7.方程x2-$\frac{1}{2}$x+$\frac{3}{2}$=0的根的情况是( )| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
分析 首先把方程转化为2x2-x+3=0,然后求出根的判别式的值,进而作出判断.
解答 解:∵原方程两边同时乘以2可以变成:2x2-x+3=0,
∴△=1-4×2×3=-23<0,
∴此方程没有实数根,
故选:C.
点评 此题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
17.八(6)班组织了一次经典朗读比赛,甲、乙两队各9人的比赛成绩如表(10分制):
(1)甲队成绩的中位数是10分,乙队成绩的众数是9分;
(2)计算乙队的平均成绩和方差;
(3)若选择其中一队参加校级经典朗读比赛则应选乙队.
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 |
(2)计算乙队的平均成绩和方差;
(3)若选择其中一队参加校级经典朗读比赛则应选乙队.
17.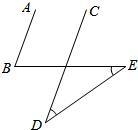 如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
 如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
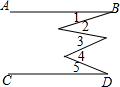 如图,AB∥CD,请猜想∠1、∠2、∠3、∠4、∠5的关系∠1+∠3+∠5=∠2+∠4.
如图,AB∥CD,请猜想∠1、∠2、∠3、∠4、∠5的关系∠1+∠3+∠5=∠2+∠4.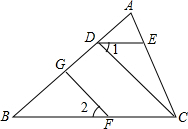 如图,已知DE∥BC,∠1=∠2,FG⊥AB,垂足为G,试说明CD⊥AB.
如图,已知DE∥BC,∠1=∠2,FG⊥AB,垂足为G,试说明CD⊥AB.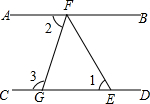 如图,直线AB∥CD,点F在直线AB上,点G、E在直线CD上,FE平分∠BFG,且∠1=50°,求∠2与∠3的度数.
如图,直线AB∥CD,点F在直线AB上,点G、E在直线CD上,FE平分∠BFG,且∠1=50°,求∠2与∠3的度数.
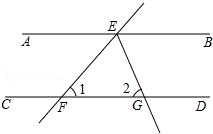 如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于( )
如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于( )