题目内容
1．
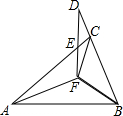如图，已知△ABF≌△ACF≌△DBF，∠FAB：∠ABF：∠AFB=4：7：25，则∠AED的度数为130°．
分析 根据题意和三角形内角和定理分别求出∠FAB、∠ABF、∠AFB的度数，根据全等三角形的性质得到∠DFB=∠AFB=125°，根据三角形的外角的性质计算即可．
解答 解：设∠FAB、∠ABF、∠AFB分别为4x、7x、25x，
则4x、7x、25x=180°，
解得x=5°，
则∠FAB、∠ABF、∠AFB分别为20°、35°、125°，
∵△ABF≌△ACF≌△DBF，
∴∠DFB=∠AFB=125°，
∴∠AFE=110°，
∴∠AED=∠CAF+∠AFE=130°，
故答案为：130°．
点评 本题考查的是全等三角形的性质，掌握全等三角形的对应边相等、对应角相等是解题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
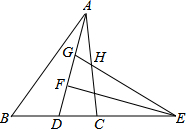如图，在△ABC中，5AB=6AC，AD为△ABC的角平分线，点E在BC的延长线上，EF⊥AD于点F，点G在AF上，FG=FD，连接EG交AC于点H．若点H是AC的中点，则$\frac{AG}{FD}$的值为$\frac{10}{7}$．
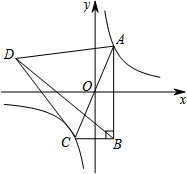如图，已知双曲线y=$\frac{k}{x}$（k≠0）与正比例函数y=mx（m≠0）交于A、C两点，以AC为边作等边三角形ACD，且S△ACD=20$\sqrt{3}$，再以AC为斜边作直角三角形ABC，使AB∥y轴，连接BD．若△ABD的周长比△BCD的周长多4，则k=（ ）
9．在实数-5，$\frac{1}{2}$，-2，8，0，3.14中，属于正数的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
16．直线l：y=3x经过平移得到直线l2，直线l2经过点（m，n），且m，n满足关系6m-2n=-4，则l2是由l1（ ）
| A． | 向上平移2个单位长度得到的 | B． | 向上平移4个单位长度得到的 | ||
| C． | 向下平移2个单位长度得到的 | D． | 向下平移4个单位长度得到的 |
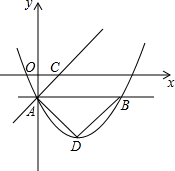如图，抛物线y=ax2+bx-1（a≠0）的对称轴是直线x=2，最低点D的纵坐标为-3，A，B为抛物线上的两点，且直线AB∥x轴．
如图，在平面直角坐标系中，⊙A经过原点O，并且分别与x轴、y轴交于B、C两点．已知B（24，0），C（0，10），则⊙A的半径为13．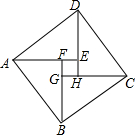
如图，由四个全等的直角三角形拼成“赵爽弦图”． Rt△ABF中，∠AFB=90°，AF=3，AB=5．四边形EFGH的面积是1．