题目内容
10.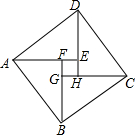 如图,由四个全等的直角三角形拼成“赵爽弦图”. Rt△ABF中,∠AFB=90°,AF=3,AB=5.四边形EFGH的面积是1.
如图,由四个全等的直角三角形拼成“赵爽弦图”. Rt△ABF中,∠AFB=90°,AF=3,AB=5.四边形EFGH的面积是1.
分析 根据勾股定理可求出BF,易证四边形EFGH是正方形,只需求出该正方形的边长,就可解决问题.
解答 解:∵∠AFB=90°,AF=3,AB=5,
∴BF=4.
由题可得DE=CH=BG=AF=3,AE=DH=CG=BF=4,
∴EF=FG=GH=EH=4-3=1.
∴四边形EFGH是菱形.
∵∠EFG=180°-90°=90°,
∴菱形EFGH是正方形,
∴正方形EFGH的面积是1.
故答案为1.
点评 本题主要考查了正方形的判定、勾股定理、正方形的面积等知识,证到四边形EFGH是正方形是解决本题的关键.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | a3+a4=a7 | B. | 2a3•a4=2a7 | C. | 2(a4)3=2a7 | D. | a8÷a4=a2 |
2.2013年10月27日CCTV Music Radio音乐之声“让爱回家”石家庄站在石家庄某商场举办公益活动,在某一时段内,小丽统计捐款金额和捐款人数如下表所示:
则以下说法正确的是( )
| 金额/元 | 100 | 200 | 500 | 1000 |
| 人数 | 4 | 3 | 2 | 1 |
| A. | 众数是100,中位数是200 | B. | 众数是200,中位数是500 | ||
| C. | 平均数是300,方差是400 | D. | 平均数是400,方差是300 |
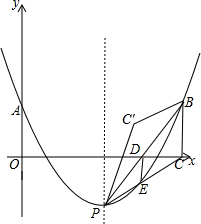 如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
如图,抛物线y=a(x-$\sqrt{2}$m)2-m(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.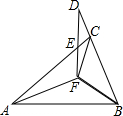 如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25,则∠AED的度数为130°.
如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25,则∠AED的度数为130°.