题目内容
6.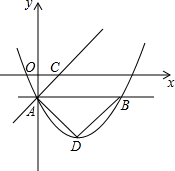 如图,抛物线y=ax2+bx-1(a≠0)的对称轴是直线x=2,最低点D的纵坐标为-3,A,B为抛物线上的两点,且直线AB∥x轴.
如图,抛物线y=ax2+bx-1(a≠0)的对称轴是直线x=2,最低点D的纵坐标为-3,A,B为抛物线上的两点,且直线AB∥x轴.(1)求抛物线的解析式;
(2)求证:△ABD是等腰直角三角形;
(3)直线AB绕点A逆时针方向旋转45°,与x轴交于点C.
①求直线AC的解析式;
②若P是线段BD上的动点,Q是线段OC上的动点,试判断在点P和点Q的移动过程中,△PAQ的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
分析 (1)求得抛物线的顶点坐标,设出顶点式展开和一般式比较求得a、b即可;
(2)利用二次函数的对称性得出AD=DB,利用勾股定理得出AD,DB,AB进一步判定三角形的形状即可;
(3)①得出△OAC是等腰直角三角形,求得点C坐标,利用待定系数法求函数解析式;
②利用对称性得出点A关于x轴与BD的对称点,利用勾股定理和对称的性质求得最小值即可.
解答 解:(1)∵抛物线的顶点坐标为(2,-3),
∴设抛物线的解析式为y=a(x-2)2-3,
即y=ax2-4ax+4a-3,
∵抛物线y=ax2+bx-1,
∴b=-4a,4a-3=-1,
∴a=$\frac{1}{2}$,b=-2,
∴抛物线y=$\frac{1}{2}$x2-2x-1;
(2)由题意可知DA=DB,
∵点D坐标为(2,-3),
∴AB=4,AD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴DB=2$\sqrt{2}$,
∴△ABD是等腰直角三角形.
(3)①∵点A坐标为(0,-1),△OAC是等腰直角三角形,
∴OC=OA=1,
∴点C坐标为(1,0),
∴直线AC的解析式为y=x-1.
②存在最小值为2$\sqrt{13}$.
如图,
作点A关于x轴的对称点A′,作点A关于直线BD的对称点A″,
连接A′A″交BD于点P,交OC于点Q,连接AP,AQ,此时的△PAQ为符合题意的周长最小的三角形.
∵A、A′关于x轴对称,
∴点A′的坐标为(0,1),
∵A、A″关于x轴对称,△ABD是等腰直角三角形,
∴△A″DB是等腰直角三角形,
∴△A″AB是等腰直角三角形,
∴点A″的坐标为(4,-5),
过点A″作A″E⊥y轴于点E,
∴A′E=6,
在直角△A′A″E中,
A′A″=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
∴点P和点Q的移动过程中,△PAQ的周长存在最小值,最小值为2$\sqrt{13}$.
点评 此题考查二次函数综合题,掌握待定系数法求函数解析式,等腰直角三角形的性质,勾股定理以及利用对称性求最值是解决问题的关键.

| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ① |
| A. | 1 | B. | -1 | C. | ±1 | D. | 16216729 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
| A. | 3a2-2a=a | B. | (-a2)3=a6 | C. | a÷a3=$\frac{1}{{a}^{2}}$ | D. | 2a2•3a2=5a4 |
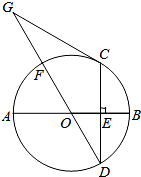 如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°
如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°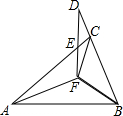 如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25,则∠AED的度数为130°.
如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25,则∠AED的度数为130°.